只含有一個未知數,並且未知數項的最高次數是4的整式方程叫做一元四次方程。
一元四次方程的一般形式是ax4+bx3+cx2+dx+e=0(a,b,c,d,e∈R,且a≠0)。
基本介紹
- 中文名:一元四次方程
- 外文名:Quartic equation of one unknown
- 解釋:只有一個未知數,最高為4次
- 學科:數學
- 一般式:ax^4+bx^3+cx^2+dx+e=0(a,b,c,d,e∈R,且a≠0)
滿足條件,方程形式,常用解法,費拉里法,笛卡爾法,計算公式,費拉里法,求根公式(費拉里法),求根公式(planetmath),計算程式代碼,費拉里法(VC++),驗算代碼(VC++),
滿足條件
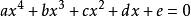
(a,b,c,d,e∈R,且a≠0)
一元四次方程必須滿足以下三個條件:
②只含有一個未知數;
③未知數項的最高次數是4(即a≠0)。
註:如果方程滿足條件①,化簡後不滿足條件②和③,則該方程不是一元四次方程。
方程形式
一般形式:
ax4+bx3+cx2+dx+e=0(a,b,c,d,e∈R,且a≠0)
 一元四次方程的四個根(root)
一元四次方程的四個根(root)通常我們也把它寫成四次項係數為1的形式:
x4+bx3+cx2+dx+e=0(b,c,d,e∈R)
常用解法
費拉里法
方程兩邊同時除以四次項的係數可得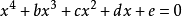 (1)
(1)
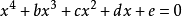
移項可得 x4+bx3=-cx2-dx-e (2)
兩邊同時加上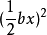 ,可將(2)式左邊配成完全平方,
,可將(2)式左邊配成完全平方,
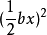
方程成為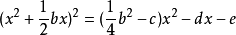 (3)
(3)
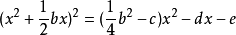
在(3)式兩邊同時加上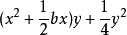
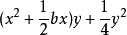
可得
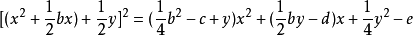
(4)式中的y是一個參數。當(4)式中的x為原方程的根時,不論y取什麼值,(4)式都應成立。
特別,如果所取的y值使(4)式右邊關於x的二次三項式也能變成一個完全平方式,則對(4)對兩邊同時開方可以得到次數較低的方程。 為了使(4)式右邊關於x的二次三項式也能變成一個完全平方式,只需使它的判別式變成0,即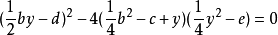 (5)
(5)
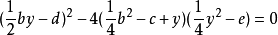
把由(5)式求出的y值代入(4)式後,(4)式的兩邊都成為完全平方,兩邊開方,可以得到兩個關於x的一元二次方程。
解這兩個一元二次方程,就可以得出原方程的四個根。
費拉里法經過簡化後,實際上可以這樣表述:
先將一元四次方程化為x4+bx3+cx2+dx+e=0
此方程是以下兩個一元二次方程的解:
2x2+(b+M)x+2(y+N/M)=0
2x2+(b-M)x+2(y-N/M)=0
其中
M=√(8y+b2-4c);N=by-d,(M≠0)
y是一元三次方程8y3-4cy2-(8e-2bd)y-e(b2-4c)-d2=0的任一實根。
費拉里發現的上述解法的創造性及巧妙之處在於:第一次配方得到(3)式後引進參數y,並再次配方把(3)式的左邊配成含有參數y的完全平方,即得到(4)式,再利用(5)式使(4)的右邊也成為完全平方,從而把一個一元四次方程的求解問題化成了一個一元三次方程及兩個一元二次方程的求解問題。 不幸的是,就象塔塔利亞發現的一元三次方程求根公式被誤稱為卡當公式一樣,費拉里發現的一元四次方程求解方法也曾被誤認為是波培拉發現的。
笛卡爾法
先將四次方程化為x4+ax3+bx2+cx+d=0的形式。
令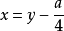 ,整理後得到
,整理後得到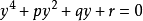 (1)
(1)
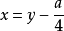
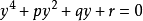
設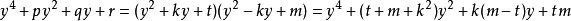
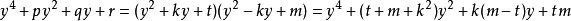
比較dy對應項係數,得t+m-k2=p,k(m-t)=q,tm=r
設k≠0,把t和m當作未知數,解前兩個方程,得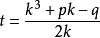 ,
,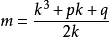
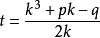
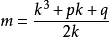
再代入第三個方程,得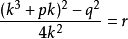 。即k6+2pk4+(p2-4r)k2-q2=0
。即k6+2pk4+(p2-4r)k2-q2=0
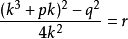
解這個方程,設k0是它的任意一根,t0和m0是k=k0時t和m的值那么方程(1)就成為
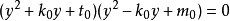
解方程y2+k0y+t0=0和y2-k0y+m0=0就可以得出方程(1)的四個根,各根加上-a/4就可以得出原方程的四個根。
計算公式
費拉里法
費拉里法求解一元四次方程 的步驟如下
的步驟如下

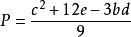
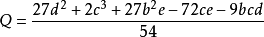
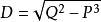
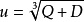
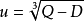
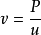
y有三種取值
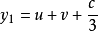

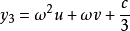
上面兩個公式中,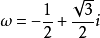 ,
,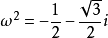
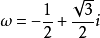
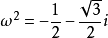
將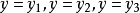 分別代入
分別代入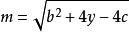 ,就能得到三組(y,m)。請選擇
,就能得到三組(y,m)。請選擇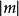 最大或
最大或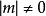 的一組作為 y,m 的數值。
的一組作為 y,m 的數值。
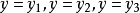
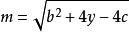
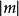
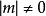
若m=0則一元四次方程有兩對重根,計算公式如下:
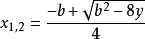
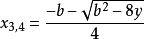
若 m 不等於零,則一元四次方程的求根公式如下:
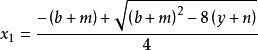
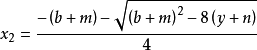
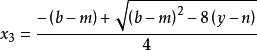

算例1: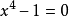
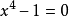
上式中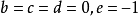 ,可算得
,可算得
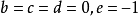
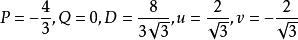
y 取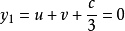 時,m = 0。這個 y 不合適,換一個再試試
時,m = 0。這個 y 不合適,換一個再試試
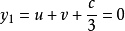
y 取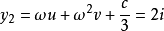 時,
時,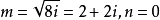 可算得四個根為
可算得四個根為
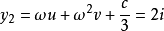
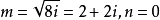
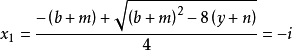
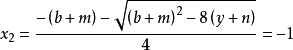
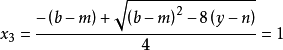
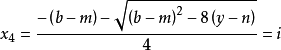
算例2: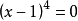 即
即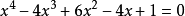
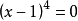
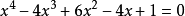
上式中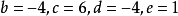 ,可算得
,可算得
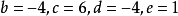
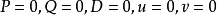
y 有三重根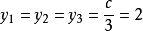 ,可算得 m = 0。
,可算得 m = 0。
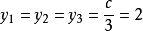
因此,一元四次方程有兩對重根,即

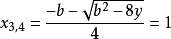
求根公式(費拉里法)
對費拉里計算方法整理後,即可得到一元四次方程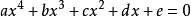 的求根公式
的求根公式
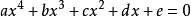

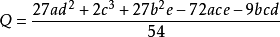
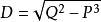
如果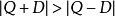 那么
那么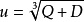 否則
否則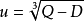
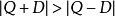
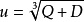
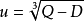
若 u 不為零,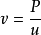 ,否則 v 為零
,否則 v 為零
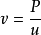
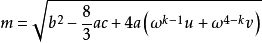
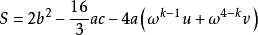
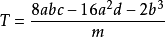
上面三個公式中的 k 可取值1,2,3,用來區別費拉里法中一元三次方程的三個根。請選擇  最大的那組(m,S,T)。
最大的那組(m,S,T)。

如果  的最大值仍為零,則
的最大值仍為零,則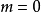 ,
,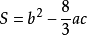 ,
,

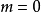
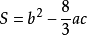

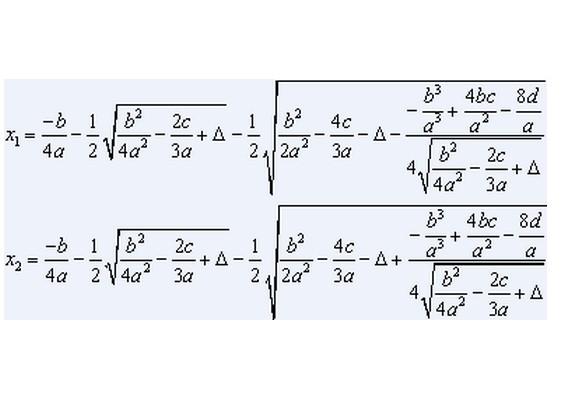
一元四次方程的四個根為:

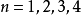
求根公式(planetmath)
網站planetmath.org上列出了方程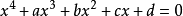 的求根公式
的求根公式
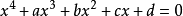
查看這個公式,需要非常的耐心和細心。將其分拆後,可以得到如下公式:

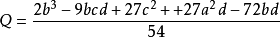
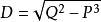
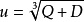
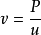

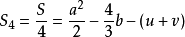
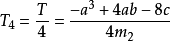
四個根為(n = 1,2,3,4)
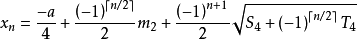
可見,這個公式是“求根公式(費拉里法)”的一個特例。
這個公式不僅複雜,而且有很多問題:
1、當 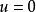 時
時 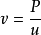 會計算失敗;
會計算失敗;
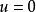
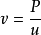
2、當 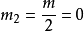 時,求根計算會失敗。
時,求根計算會失敗。
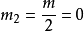
計算程式代碼
費拉里法(VC++)
#include <math.h> #include <float.h> #include <complex.h> /******************************************************************************\ 對一個複數 x 開 n 次方 \******************************************************************************/ std::complex<double> sqrtn(const std::complex<double>&x,double n) { double r = _hypot(x.real(),x.imag()); //模 if(r > 0.0) { double a = atan2(x.imag(),x.real()); //輻角 n = 1.0 / n; r = pow(r,n); a *= n; return std::complex<double>(r * cos(a),r * sin(a)); } return std::complex<double>(); } /******************************************************************************\ 使用費拉里法求解一元四次方程 a*x^4 + b*x^3 + c*x^2 + d*x + e = 0 \******************************************************************************/ void Ferrari(std::complex<double> x[3] ,std::complex<double> a ,std::complex<double> b ,std::complex<double> c ,std::complex<double> d ,std::complex<double> e) { a = 1.0 / a; b *= a; c *= a; d *= a; e *= a; std::complex<double> P = (c * c + 12.0 * e - 3.0 * b * d) / 9.0; std::complex<double> Q = (27.0 * d * d + 2.0 * c * c * c + 27.0 * b * b * e - 72.0 * c * e - 9.0 * b * c * d) / 54.0; std::complex<double> D = sqrtn(Q * Q - P * P * P,2.0); std::complex<double> u = Q + D; std::complex<double> v = Q - D; if(v.real() * v.real() + v.imag() * v.imag() > u.real() * u.real() + u.imag() * u.imag()) { u = sqrtn(v,3.0); } else { u = sqrtn(u,3.0); } std::complex<double> y; if(u.real() * u.real() + u.imag() * u.imag() > 0.0) { v = P / u; std::complex<double> o1(-0.5,+0.86602540378443864676372317075294); std::complex<double> o2(-0.5,-0.86602540378443864676372317075294); std::complex<double>&yMax = x[0]; double m2 = 0.0; double m2Max = 0.0; int iMax = -1; for(int i = 0;i < 3;++i) { y = u + v + c / 3.0; u *= o1; v *= o2; a = b * b + 4.0 * (y - c); m2 = a.real() * a.real() + a.imag() * a.imag(); if(0 == i || m2Max < m2) { m2Max = m2; yMax = y; iMax = i; } } y = yMax; } else {//一元三次方程,三重根 y = c / 3.0; } std::complex<double> m = sqrtn(b * b + 4.0 * (y - c),2.0); if(m.real() * m.real() + m.imag() * m.imag() >= DBL_MIN) { std::complex<double> n = (b * y - 2.0 * d) / m; a = sqrtn((b + m) * (b + m) - 8.0 * (y + n),2.0); x[0] = (-(b + m) + a) / 4.0; x[1] = (-(b + m) - a) / 4.0; a = sqrtn((b - m) * (b - m) - 8.0 * (y - n),2.0); x[2] = (-(b - m) + a) / 4.0; x[3] = (-(b - m) - a) / 4.0; } else { a = sqrtn(b * b - 8.0 * y,2.0); x[0] = x[1] = (-b + a) / 4.0; x[2] = x[3] = (-b - a) / 4.0; } } |
驗算代碼(VC++)
void Test_QuarticEquation() { std::complex<double> x[4]; std::complex<double> x1(2.0,0.0); //隨便填 std::complex<double> x2(2.0,0.0); //隨便填 std::complex<double> x3(2.0,0.0); //隨便填 std::complex<double> x4(2.0,0.0); //隨便填 std::complex<double> a ( 1.0,0.0); //隨便填(不為零即可) std::complex<double> b = a * (-x1-x2-x3-x4); std::complex<double> c = a * (x1 * x2 + x1 * x3 + x1 * x4 + x2 * x3 + x2 * x4 + x3 * x4); std::complex<double> d = a * (-x2 * x3 * x4 - x1 * x3 * x4 - x1 * x2 * x4 - x1 * x2 * x3); std::complex<double> e = a * (x1 * x2 * x3 * x4); Ferrari(x,a,b,c,d,e); //驗證費拉里法 } |