基本介紹
定義
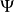
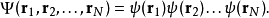
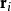
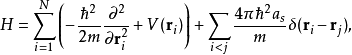
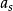

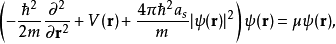
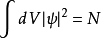
方程形式
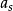

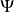
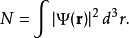
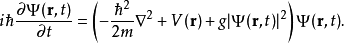
方程解
精確解
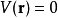
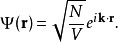
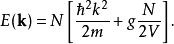

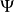
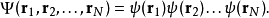
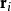
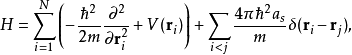
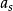

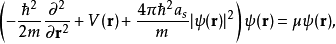
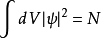
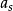

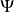
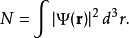
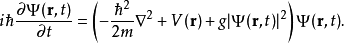
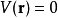
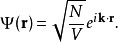
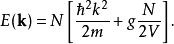
Gross–Pitaevskii 方程(以Eugene P. Gross命名與Lev Petrovich Pitaevskii) 描述了全同玻色子量子體系的基態,其中使用了Hartree-Fock近似與贗勢相互作用模型。...
金茲堡-朗道方程,或金茲堡-朗道理論,是由維塔利·金茲堡和列夫·朗道在1950年提出...Gross-Pitaevskii方程 反應-擴散系統 塞伯格-維騰理論 拓撲缺陷 ...
《玻色:愛因斯坦凝聚中的量化渦旋及其動力學》的特點與獨到之處是我們設計了一種模守恆且能量遞減的數值方法來求得靜態的Gross-Pitaevskii方程(組)的數值解;我們也...
1.4 離散的Gross-Pitaevskii方程及等效經典哈密頓表示參考文獻第2章 雙勢阱BEC的非線性量子隧穿2.1 非線性Josephson周期振盪2.2 通向自囚禁的量子相變...
接著從三維的非線性薛丁格方程(Gross-Pitaevskii方程)出發,推導出一維的非線性薛丁格方程,可以很好的描述漏斗勢中超冷玻色氣體的軸向動力學。最後討論了在實驗上實現...
5. 中央高校基本科研業務費項目,FRF-TP-14-069A2、一類非局部Gross-Pitaevskii方程組解的爆破門檻和真空隔離現象,2014/09-2015/08、已結題、主持。 [1] ...
2015.01-2015.12Gross-Pitaevskii方程精確解及孤子動力學性質研究,參與人 2/52014.08-2016.12極化子效應對低維量子系統非線性光學特性的影響,參與人4/4[1] ...
最後,基於規範勢分解以及Gross-Pitaevskii方程的幾何化思想,論文提出了Bose-Einstein凝聚體的有效規範動力學。對旋轉勢阱中的Bose凝聚體,給出了具體的基態和一個穩定...
