齊次線性方程組:常數項全部為零的線性方程組。如果m<n(行數小於列數,即未知數的數量大於所給方程組數),則齊次線性方程組有非零解,否則為全零解。
基本介紹
- 中文名:齊次線性方程組
- 外文名:homogeneous linear equations
- 學科:線性代數
- 屬性:常數項全部為零的線性方程組
- 求解方法:化為階梯形矩陣再求解
- 相關名詞:非齊次線性方程組
- 作用:判斷是否有非零解
公式簡介
定義

- 當r=n時,原方程組僅有零解;
- 當r<n時,有無窮多個解(從而有非零解)。
證明
示例
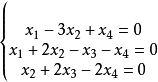

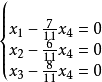

判定定理
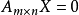
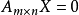
結構
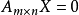
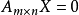
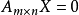
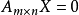

齊次線性方程組:常數項全部為零的線性方程組。如果m<n(行數小於列數,即未知數的數量大於所給方程組數),則齊次線性方程組有非零解,否則為全零解。

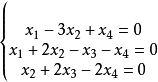

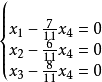

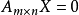
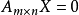
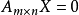
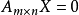
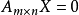
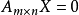
齊次線性方程組:常數項全部為零的線性方程組。如果m<n(行數小於列數,即未知數的數量大於所給方程組數),則齊次線性方程組有非零解,否則為全零解。...
線性方程組是各個方程關於未知量均為一次的方程組(例如2元1次方程組)。對線性方程組的研究,中國比歐洲至少早1500年,記載在公元初《九章算術》方程章中。線性方程...
三元齊次線性方程組(system of ternary homogeneous linear equations)亦稱三元一次齊次方程組,是一種特殊的線性方程組,即方程組中的各個方程的常數項都是零的三元...
線性方程組的解的一般形式,又稱為一般解。...... 1. 對於齊次線性方程組設齊次線性方程組 的一個基礎解係為 ,稱 為 的通解或一般解,其中 為任意常數, , ...
定理2 設非齊次線性方程組Ax=b的係數矩陣A= ,若rankA=n,則(1) 矩陣ATA是對稱正定矩陣;(2) n階線性方程組ATAx=ATb有唯一的解。...
此外,當這個齊次線性方程組的係數矩陣是一個方陣時,這個係數矩陣存在行列式為0,即有非零解,從而 線性相關。線性相關注意 編輯 對於任一向量組而言,,不是線性無關...
概念將非齊次線性方程組右端的常數項換為零,得到的齊次線性方程組,稱為該非齊次線性方程組的導出齊次線性方程組或相應的齊次線性方程組,簡稱為導出組。即為齊次...
解空間是指齊次線性方程組所有解的集合構成一個向量空間,也就是一個集合。...... 解空間是指齊次線性方程組所有解的集合構成一個向量空間,也就是一個集合。...
解向量是線性方程組的一個解。因為一組解在空間幾何里可以表示為一個向量,所以叫做解向量。解向量在矩陣和線性方程組中是常用概念。如果n元齊次線性方程組Ax=0的...
齊次線性方程組的解集的極大線性無關組稱為該齊次線性方程組的基礎解系。基礎解系是線性無關的,簡單的理解就是能夠用它的線性組合表示出該方程組的任意一組解,...
克萊姆法則,又譯克拉默法則(Cramer's Rule)是線性代數中一個關於求解線性方程組的定理。它適用於變數和方程數目相等的線性方程組,是瑞士數學家克萊姆(1704-1752)...
增廣矩陣(又稱擴增矩陣)就是在係數矩陣的右邊添上一列,這一列是線性方程組的等號右邊的值。...
題型訓練第四章 線性議程組內容概要與重難點提示考核知識要點講解一、線性方程組的各種表達形式及相關概念二、基礎解系的概念及其求法三、齊次方程組有非零解的判定...
三元齊次線性方程組詞條標籤: 科學, 學科 圖集 數學名詞圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:37次歷史版本 最近更新: 第二號帥哥 ...
(λiE-A)X=θ是齊次方程,λi均會使|λiE-A|=0,(λiE-A)X=θ必存在非零解,且有無窮個解向量,(λiE-A)X=θ的基礎解系以及基礎解系的線性組合都是...
第二步:求出特徵方程的全部根,即為的全部特徵值;第三步:對於的每一個特徵值,求出齊次線性方程組:的一個基礎解系,則的屬於特徵值的全部特徵向量是...
