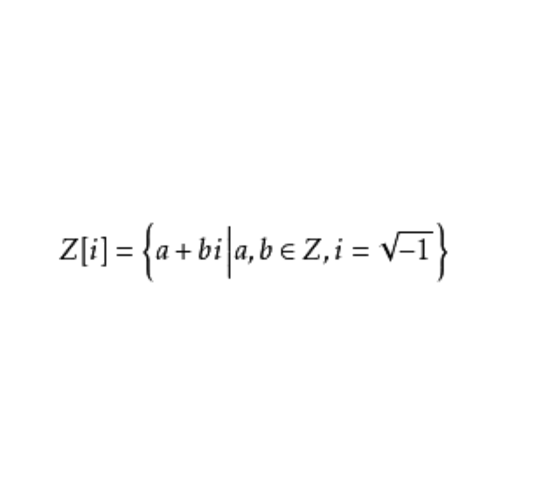高斯整數環(ring of Gauss integers)是歐氏環的一個著名例子。設Z[i]={a+bi | a,b是整數，i為虛數單位}。 Z[i]對通常數的加法和乘法構成一個整環，稱為高斯整數環。而將a +bi → a2+b2是從Z[i]\{0}到非負整數集的映射，並且這個映射滿足歐氏環定義的條件，因此，Z[i]也是歐氏環。
基本介紹
- 中文名：高斯整數環
- 外文名：ring of Gauss integers
- 類別：歐式環的一個著名例子
- 定義：Z[i]對通常數的加乘法構成個整環
- 一級學科：數學
- 二級學科：環與代數
簡介,基本性質,高斯整數環中素元的形成,Z[i]中的單位,Z[i]中的素元,Z[i]中的整數素元,Z[i]中的非整數素元,
簡介
形如
的數稱為高斯整數，是高斯在研究二次不定方程時首先提出的。記
，可以證明
關於數的加法和乘法做成交換環，我們稱之為高斯整數環。另外，將高斯整數環推廣到
的情形，稱為高斯整數環的推廣環。
高斯整數環是一種構造特殊且具有一定代表性的環 ，在代數環論中占有重要的地位 。既融入了環論的思想，同時亦包含有數論的思想，對於高斯整數環的研究一直是國內外學者的重要課題之一，數學家們通過多年的研究，得出了許多重要且富有意義的結論。
基本性質
（1）高斯整數環是歐幾里德整環。
（2）高斯整數環是主理想整環。
（3）高斯整數環是唯一因式分解整環R，滿足下列兩個條件：
①因子鏈條件成立 ，即如果序列中
，每一個
是
的真因子，則這個序列是有限序列；
②每一個不可約元都是素元，則R是唯一因式分解整環。
高斯整數環中素元的形成
Z[i]中的單位
Z[i]中的素元
Z[i]中的整數素元
對於環 Z[i]，它的元素可分為兩部分，一部分是整數，另一部分是形如 a+bi（b≠0）的元素。首先討論整數集 Z中的素元。Z 中的非素數肯定不是 Z[i]中的素元 ，因為 Z[i]中的素元要求除本身及單位外無其他因子，故只有素數才可能是 Z[i]中的素元。但並非 Z中的一切素數都是 Z[i]中的素元，例如素數 2在Z[i]中可分解為
，1±i 都不是 2的相伴元，顯然它不是 Z[i]中的素元。一般的，除 2外，其他素數都可以寫成 4n+1 與4n+3 的形式，有如下定理：
（1）有理素數 p為Z[i]中素元的充分必要條件是方程 x2+y2=p 沒有整數解。
（2）形為 4n+1 類的素數為 Z[i]的非素元。
Z[i]中的非整數素元
（1）設 α∈Z[i]，若φ（α）為素數，則 α為Z[i]中的素元。
（2）若
為素數，則
①若 n=1，則α 為Z[i]中的素元；
②若 n>1，則α 為Z[i]中的非素元；
