隨機分析模型，一種非確定性分析模型，變數之間的關係是以統計值的形式給出的模型。在現實世界中，不確定現象是普遍存在的。例如，漂浮在液面上的微小粒子不斷地進行著雜亂無章運動，粒子在任一時刻的位置是不確定的；又如公共汽車站等車的人數在任一時刻也是不確定的，因為隨時都可能有乘客的到來和離去。這類不確定現象，表面看來無法把握，其實，在其不確定的背後，往往隱藏著某種確定的機率規律，因此，以機率與數理統計為基礎的隨機分析模型就成為解決此類問題最有效的工具之一。
基本介紹
- 中文名：隨機分析模型
- 外文名：Stochastic Analysis Model
- 領域：信息科學
- 分類：分析模型
- 理論：機率論與數理統計
- 套用：金融、醫學、保險等
模型介紹,理論基礎,鞅論,泊松過程,Wiener過程,伊藤過程,套用實例,風力發電系統,光伏發電系統,配電負荷,意義,
模型介紹
從實際問題抽象出一個物理模型或者說給實際問題建立一個物理模型，是許多實際問題分析建模工作中的關鍵內容。依隨機規律是否隨時間的變化而變化，隨機分析模型可分為靜態和動態兩類，前者只涉及到隨機變數（向量）的機率分布及其數字特徵，後者則要處理隨機過程和隨機微分方程。
隨機模型是試驗的各處理皆是隨機抽自
的一組隨機樣本，因而處理效應τ是隨機的，隨試驗的不同而不同。若重複做試驗，必然是從總體 中隨機抽取一組新的樣本。其分析的目的不在於研究處理效應，而是在於研究τ的變異度，故推斷也不是關於某些供試處理，而是關於抽出這些處理的整個總體。
理論基礎
鞅論
鞅論分為離散鞅和連續鞅，是由美國數學家杜布建立的一套數學理論，其中包括的基本概念和重要定理有：上鞅、下鞅、停時定理、鞅收斂定理、鞅不等式、鞅差列的強大數律、鞅的中心極限定理等。數學上，鞅論可以套用在調和函式與下調和函式研究方面，是隨機過程與數理統計研究的有力工具。本質上，鞅是一個過程，這個過程可以理解為一個進行公平賭博的賭徒的財富（變化）情況，廣泛套用於金融、醫學以及保險等行業的實際問題中。
定義
如果隨機過程
滿足以下兩個條件：
1. 對於
的任何n，
；
2.
則稱隨機過程為鞅。在鞅理論中，關鍵問題就是找到鞅測度或者等價鞅測度，找到鞅測度或者等價鞅測度也就找到了行業套用中我們想要得到的結果。
停時定理（可選抽樣定理）
鞅停時定理的意義在於，在公平的賭博中，你不可能贏。在一個公平的博弈中，若局中人在每次賭局結束時的賭本與他開始時的賭本一樣，但他未必一直賭下去，他可以選擇任一時刻停止賭博，這一時刻是隨機的，如果要他在停止時旳賭本和他開始時的賭本相同，需要附加條件，這些條件一旦滿足就是鞅停時定理。而停時概念就蘊含其中：事件應該由某時刻以及之前的信息完全確定，而不需要也無法藉助將來的情況，且一場博弈不會無限期地延續下去，停止一個事件是隨時的。並且停止一個事件是以巳發生的事件結果為依據的。停時定理可用於確定股票期權值的界。
鞅收斂定理
鞅收斂定理說明：在很一般的條件下，鞅會收斂到一個隨機變數。這個結果很有用，例如，假設我們對某一事件發生的機率P感興趣，而對P又一無所知，那么我們就根據鞅收斂定理，可以假定P是(0, 1)上的均勻分布，幫助隨機過程的推導。
泊松過程
泊松過程是時間間隔為獨立且同時服從指數分布的隨機變數。由於該隨機變數機率分布的不同，決定著隨機過程的不同。分布為任意分布是得到的過程為計數過程，也稱為更新過程。泊松過程是一種特殊的更新過程。
如果
是Gamma更新過程，則
，n=0, 1, 2, ...，當a為正整數時，
，n=0, 1, 2, ...。特別地，當a=1時，
，n=0, 1, 2, ...，此時為泊松過程。由於更新過程的強度為
，故此更新過程強度為
，其中
。所以對於泊松過程，時間間隔
的分布為：
，其密度函式為：
。
Possion過程常見的例子有：
- 排隊論：計算到達的客戶數；
- 一個地區的降雨量；
- 裝機光電探測器的光子數；
- 自動電話交換機的接入電話數；
- 長時間內某網路伺服器的網頁請求；
- 服務台接到諮詢電話的次數。
Wiener過程
維納過程(Wiener Process)是一個重要的獨立增量過程，也稱作布朗運動過程。
當隨機過程
滿足下列條件時，我們稱隨機過程 為布朗運動：
1. 該過程初始值為0，即；
2.
具有固定的連續增量；
3. 在時間t內連續；
4. 增量
服從均值為0，方差為|t-s|的常態分配，即：
。
伊藤過程
伊藤過程是日本數學家伊藤發展建立的帶有布朗運動干擾項的隨機微分方程，可看成為一般化的維納過程。隨機過程
，如果其微分形式可以表示為：
，其中dz是Wiener過程，則稱 為一個伊藤過程。伊藤引理表明，如果隨機變數x遵循伊藤過程，設
是x和t的二階連續可微函式，則
遵循如下過程：
。
套用實例
風力發電系統
威布爾（Weibull）分布雙參數曲線用於擬合風速分布的線型，其機率密度函式可表達為：
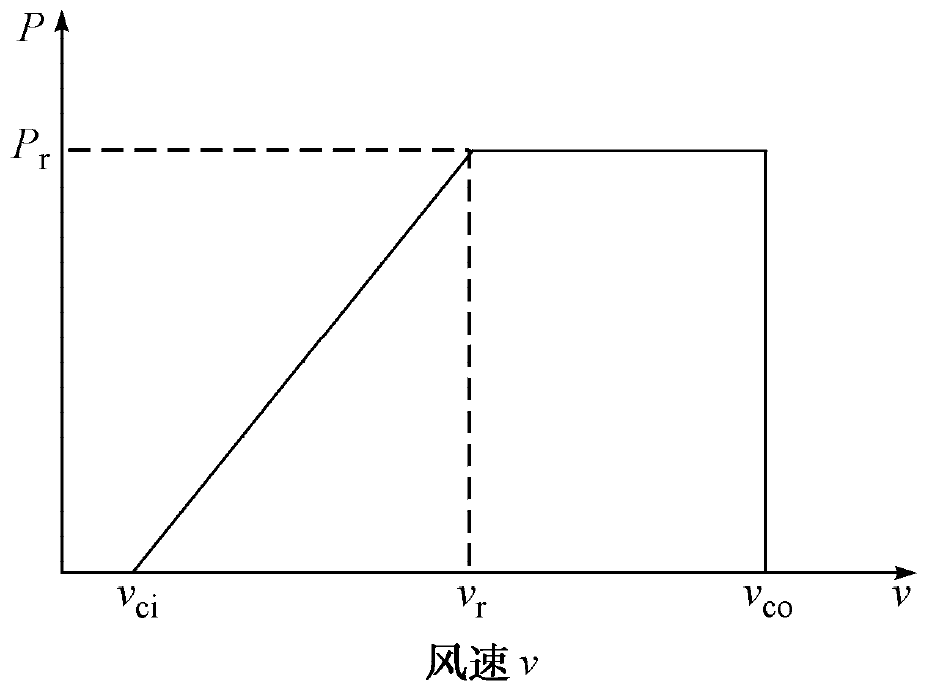圖1 風力發電勸率輸出曲線式中：v為風速；k和c分別為Weibull分布的形狀參數、適度參數，μ為平局風速，σ為標準差。
當知道了風速的分布之後，就可以通過風力發電機組的輸出功率與風速之間的近似關係得到輸出功率的隨機分布。風力發電機出力與風速之間的函式關係如圖1所示。其中
為風力發電機額定功率，
為切入風速，
為額定風速，
為切出風速。由圖1可以得到風力發電輸出功率
與風速v之間的函式關係式：
經統計，大部分時間內風速維持在 和
之間，
與v近似成一次函式關係，因此可求出風力發電有功功率機率密度如下：
風力發電機可簡化處理為PQ節點，假定通過風電機組中電容器的自動投切，可使功率因數恆定不變。這樣，無功功率為：
，式中：φ為功率因數角，對併網風電機而言，φ一般位於第4象限，tanφ為負值。
光伏發電系統
太陽能電池是光伏發電系統的基礎和核心，它的輸出功率與光照強度密切相關，由於光強具有隨機性 因此輸出功率也是隨機的，據統計，在一定時間段內（1h或幾h），太陽光照強度可以近似看成貝塔分布(Beta Distribution)，其機率密度函式如下：
式中：r和
分別為這一時間段內的實際光強和最大光強；α，β均為Beta分布的形狀參數。
假設給定一太陽能電池仿真，具有M個電池組件，每個組件的面積和光電轉換效率分別為
，於是這個太陽能電池方陣總的輸出功率為
，式中：A為方陣總面積η為方陣總的光電轉換效率，它們分別為：
已知光強的機率密度函式，可以得到太陽能電池方陣輸出功率的機率密度函式也呈Beta分布：
式中：
為方陣最大輸出功率。與風力發電類似，光伏發電系統也由電容器組來保證功率因數基本為一常數，因此在潮流計算中可看做PQ節點，其隨機分布也呈Beta分布。
配電負荷
多數有關隨機潮流的文獻均將負荷預測結果看做一個隨機變數，並採用常態分配近似反映負荷的不確定性。假設負荷實部和虛部參數分別是
和
，其實部和虛部的機率密度函式分別為：
式中：μ為數學期望，
為方差。
意義
金融、醫學、保險等行業具有較高的複雜性和多樣性，給的行業實際問題的分析研究帶來很大麻煩，隨機分析模型正是用於這些複雜性問題的分析，給行業實際問題研究帶來巨大幫助。
