階乘數定理

階乘數定理是由fxccommercial 本人發現並歸納整理的一個新的數學定理猜想，但目前關於這個定理的證明尚無人能給出。

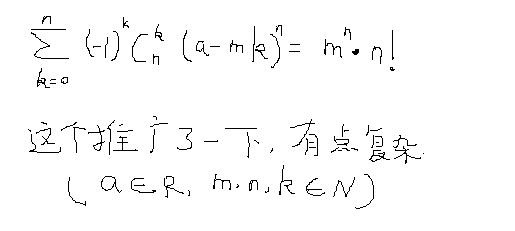
猜想提出

由fxccommercial 提出，系fxccommercial 本人發現並歸納整理成為一個新的數學定理猜想（2006.09.27）。這個公式描述的是，從大到小排列的n+1個等差數列，對每個數取n次方，用（-1）^n*C(n,k）做係數，實現奇偶項數的差項和，則這列數的和為n！，目前fxccommercial 已得到一個關於他的推論，經驗證是正確的。歷史上並沒有人得到過類似的公式，可以認為它是人類對數學的又一個深刻的認識，但目前關於這個定理的證明尚無人能給出，筆者期待這個定理證明的解決。

約定∑_k=0_n 表示對從0到n的n+1項求和,則該定理表述為：

公式Ⅰ ∑_k=0_n (-1）^k*C(n,k)*(a-m*k)^n = m^n*n! (a,m屬於R; n為正整數）

n^k：n的k 次方；

n！：n的階乘；

C(n,k）：組合數，表示n個元素里取k個元素的組合種類數。

定理證明

我在幾天前搜尋階乘數（完全的另外一個概念）時，看到了此詞條，掃了一眼，和女友聊天時提到了該詞條，第二天她告訴我原定理（a=0時）可以用等價概念的方法來證明，我整理了一下在此給出具體的證明過程。

首先，我們把原公式稍作修改：兩邊同時除以m^n，然後把因子（a/m-k）取相反數，使k的係數為正，最後令b=a/m，則公式Ⅰ等價化為：

公式Ⅱ

∑（-1）^(n-k)*C(n,k)*(k-b)^n = n! (n為正整數，∑是關於k從0到n求和，b是任意實數）

現在，我們來看另外一個問題：有n個數字，n個位置，則這n個數字可重複的排列在這n個位置上，其排列數為n^n，我們把所有的這些排列看成一個總的集合T。設Ai 表示不包含數字i 的所有排列組成的集合，則容易得Ai 的大小 |Ai | = (n-1）^n，1=< i <=n。設集合F是這n個Ai 補集的交集，即F=∩￢Ai，則在這裡F正好表示的是n個數字全排列組成的集合（大小為n！）。利用摩根公式有：

公式Ⅲ

F=∩￢Ai=￢（∪Ai)=T\（∪Ai) ，∩、∪是關於i 從1到n求交、並。

我們來看集合∪Ai 的大小，根據集合的容斥原理有：

|∪Ai | = ∑ |Ai | - ∑ |Ai ∩Aj | + ∑ |Ai ∩Aj ∩Ak | - ... + (-1）^(n-1）* |A1 ∩A2 ∩...∩An |

∑ |Ai ∩Aj |，Ai ∩Aj 表示不包含i 和j 這兩個數字的排列（大小為（n-2）^n），則∑ |Ai ∩Aj | = C(n,2）*(n-2）^n，同樣的也可得出其他項的數值，所以：

|∪Ai | = C(n,1）*(n-1）^n - C(n,2）*(n-2）^n +...+ (-1）^(n-1）*C(n,n)*0^n = ∑（-1）^(n-1-k)*C(n,k)*k^n ，∑是關於k從0到n-1求和。

對公式Ⅲ兩邊求集合大小：

n! = |F | = |T\（∪Ai) | = |T | - |∪Ai | = ∑（-1）^(n-k)*C(n,k)*k^n ，∑是關於k從0到n求和。

這就證明了公式Ⅱ b=0時的情形，

證明一般情況

設函式f(n,r)=∑（-1）^(n-k)*C(n,k)*k^r ，其中r 為非負整數，上面的證明已經得到當r =n時，f(n,r)=n！，下面我們來證明當0=< r <= n-1時，f(n,r)=0。方法和上面的方法相同，只是我們現在考慮的不是有n個位置，而是有r 個位置且r <= n-1，我們可以得到：

f(n,r) =∑（-1）^(n-k)*C(n,k)*k^r = |F |

那么，根據鴿籠原理：在r <=n-1個位置放這n個數字，則至少有兩個數字相同，而集合F中的元素（排列）各個位置的數字是要互異的，也就是說集合F為空集，則|F | = 0，即f(n,r)=0。

現在我們將公式Ⅱ的（k-b)^n用二項式定理展開，第一項不含有b求和後等於n！，而k的次數r 小於等於n-1的那些項求和含有因子f(n,r)=0，因而和b的值無關，就此得到最終結果：∑（-1）^(n-k)*C(n,k)*(k-b)^n = n! (n為正整數，∑是關於k從0到n求和，b是任意實數）。

證畢