誘導叢

誘導叢(induced bundle)是指從一個纖維叢經一個連續映射誘導出的一個新的纖維叢。纖維叢是坐標叢的一個等價類。由於每一個坐標叢都惟一地決定了一個纖維叢，故通常當得到一個坐標叢時，就認為得到了一個纖維叢。

基本介紹

• 中文名：誘導叢
• 外文名：induced bundle
• 領域：數學
• 對象：纖維叢
• 方式：連續映射誘導而來
• 相關概念：誘導向量叢

概念

從一個纖維叢經一個連續映射誘導出的一個新的纖維叢。設：

為纖維叢，ψ：B′→B為連續映射，考慮E×B′的子空間：

若p′：E′→B′，Ψ：E′→E分別為乘積空間的投射：

在E′上的限制，則ψ^#ξ=(E′，p′，B′，F，G)是纖維叢，並且Ψ是由ψ^#ξ到ξ的叢映射，ψ^#ξ稱為由ψ得到的ξ的誘導叢，也稱為叢ξ由映射ψ而得到的回退。此時，若ξ的坐標鄰域族及坐標變換族為{U_α}，{g_βα}，則ψ^#ξ的相應族為{ψ(U_α)}與{g_βα°ψ}；設已給纖維叢ξ′，ξ之間的叢映射Ψ：E′→E，若ψ：B′→B為底空間之間的映射，則ξ′≡ψ^#ξ。若ξ₁=ξ₂，則ψ^#ξ₁=ψ^#ξ₂。當ψ′：B″→B′為連續映射時，

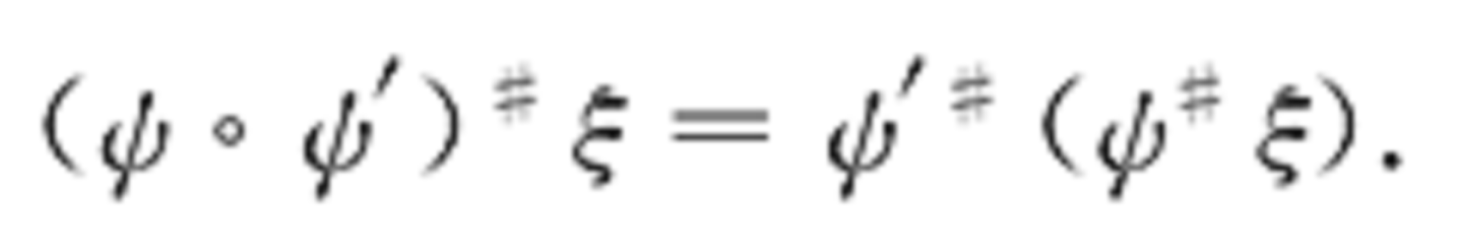
若η是主叢，則ψ^#η也是主叢。若ξ_i=(E_i，p_i，B_i，F_i，G_i}，i=1，2為纖維叢，則ξ₁×ξ₂=(E₁×E₂，p₁×p₂，B₁×B₂，F₁×F₂，G₁×G₂)在自然意義下也成為纖維叢，稱為ξ₁與ξ₂的乘積叢。特別地，若ξ_i=(E_i，p_i，B，k，GL(n_i，R))為向量叢，Δ：B→B×B，Δ(b)=(b，b)為對角映射，則誘導向量叢Δ(ξ₁×ξ₂)稱為向量叢ξ₁，ξ₂的惠特尼和，記為ξ₁⊕ξ₂，而ξ₁⊕ξ₂為B上的n₁+n₂維向量叢。誘導叢在代數拓撲中的一個重要性質是：若B′為仿緊空間，ψ₁，ψ₂：B′→B同倫，則ψ₁ξ=ψ₂ξ。

纖維叢

坐標叢的一個等價類。設給了下列事物：空間E稱為全空間，空間B稱為底空間，連續映射π：E→B稱為投影，空間F稱為典型纖維，G為作用在F上的有效拓撲變換群，稱為結構群，{V_j}_j∈J為B的開覆蓋，且對每個V_j有同胚φ_j：V_j×F→π(V_j)，(V_j，φ_j)稱為局部平凡化區圖，而{(V_j，φ_j)}稱為圖冊.若滿足下列條件，它就是一個坐標叢：

1.πφ_j(x，y)=x，對任意x∈V_j和任意y∈F；

2.令φ_j，x：F→π^-1(x)為φ_j，x(y)=φ_j(x，y)，則對任意x∈V_i∩V_j，同胚φ^-1_i，x°φ_j，x：F→F屬於G；

3.對任意i，j∈J，由g_ij(x)=φ^-1_i，x°φ_j，x定義的映射g_ij：V_i∩V_j→G連續，{g_ij}稱為轉移函式族。

坐標叢記為：(E，B，π，F，G，{(V_j，φ_j)}，{g_ij})。

對任意x∈B，記F_x=π^-1(x)，稱為點x上的纖維，它同胚於典型纖維F。

若兩個具有相同的全空間、底空間、投影、典型纖維和結構群的坐標叢的兩個轉移函式族合併起來仍滿足條件1，2和3，即仍成為一個轉移函式族，則稱這兩個坐標叢嚴格等價。

坐標叢在嚴格等價之下的一個等價類稱為一個纖維叢。

由於每一個坐標叢都惟一地決定了一個纖維叢，故通常當得到一個坐標叢時，就認為得到了一個纖維叢，且簡記為(E，B，π，F，G)，當G無需指明時也簡記為(E，B，π，F)。當F，G和π無需指明時也說E是B上的一個纖維叢。例如，若M是n維微分流形，其切叢T(M)在自然投影π之下是M上的一個纖維叢，實際上是以T(M)為全空間，M為底空間，π為投影，R為典型纖維，一般線性群GL(n，R)為結構群的纖維叢。

連續映射

設f為從拓撲空間E到拓撲空間F中的映射。稱f在E的點x0是連續的，如果對f(x₀)在F中的任一鄰域W，在E中存在x0的鄰域V，使在f下V的象包含在W中；換言之，如果在f下f(x0)的任一鄰域的逆象是x0的鄰域。

稱f在E上是連續的(或簡稱f是連續的)，如果它在E的每一點都連續。

為使f是連續的，必須且只須F的任一閉集經由f的逆象是E的閉集，或F的任一開集經由f的逆象是E的開集。但是E的開集(閉集)經由連續映射的正象不一定是F的開集(閉集)。

從E到F中的常映射是連續的.E的恆等映射是連續的。

任一從離散空間到拓撲空間的映射是連續的。

設E，F及G為拓撲空間，f為從E到F中的連續映射，而g為從F到G中的連續映射，則複合映射g°f是連續的。

當E與F為分別賦以距離d及e的度量空間時，為使f在x0點連續，其充分必要條件是：對任一嚴格正的實數ε，存在嚴格正的實數η，使得由關係d(x_，x0)≤η可推出e(f(x)，f(x0))≤ε.若f為定義在R的子集P上的有限數值函式，則使f在x0點連續的充分必要條件是：對任一嚴格正的實數ε，存在嚴格正的實數η，使得對P的任一元素x，關係|x-x₀| ≤η蘊涵|f(x)-f(x0)|≤ε。

向量叢

向量叢是流形切叢概念的抽象和推廣，它是微分拓撲學和代數拓撲學的重要研究對象。設E，B是拓撲空間(B為T₂空間)，π：E→B為連續滿映射.ξ=(E，π，B)稱為n維(實、拓撲)向量叢，若適合：

1.對於b∈B，E_b=π(b)是n維(實)向量空間；

2.(局部平凡性)對於b∈B，存在b的鄰域U及同胚映射φ：π(U)→U×R，使得對於x∈U，φ_x=φ|E_x：E_x→{x}×R是向量空間的同構。

此時，B稱為向量叢ξ的底空間，記為B(ξ)，E稱為向量叢ξ的全空間，記為E(ξ)，E_b稱為b∈B處的纖維，π稱為叢射影。上述適合條件2的(U，φ)稱為ξ的叢卡。

若∪_α∈ΛU_α=B，則稱為圖冊。進而，設B是微分流形，對於ξ的圖冊Φ，若α，β∈Λ，U_α∩U_β≠Φ，圖冊的轉換函式g_αβ：U_α∩U_β→GL(n，R)是可微的，其中g_αβ(x)=φ_βx°φ^-1_αx：Rⁿ→Rⁿ，x∈U_α∩U_β，GL(n，R)為可逆n階方陣組成的(實)線性群，則稱為可微的。若圖冊Φ是ξ的極大的可微圖冊，則ξ=(E，π，B，Φ)稱為可微向量叢。此時，若B是m維微分流形，則ξ的全空間E是(n+m)維微分流形。流形的切叢、法叢、萬有叢等都是可微向量叢的常見例子。向量叢ξ=(E，π，B)也稱為B上的向量叢。