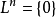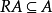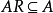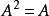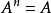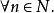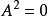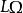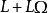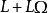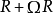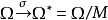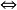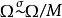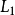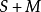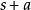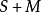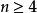詣零理想

詣零理想亦稱詣零子環，比冪零理想更廣的一類理想，它是描述克德(Kothe,G.)根的基礎，環R中元a，若有正整數n使aⁿ=0，則稱a為冪零元。適合aⁿ=0的最小正整數稱為a的冪零指數，零元的冪零指數為1，若A是環R的理想(或子環)，A中任一元皆為冪零元，則稱A為R的詣零理想，若R中每個元是冪零元，則R稱為詣零環。謝邦傑於1955年證明：左、右零化子各滿足極大條件的環的詣零子環是冪零的。八年後，林文茨基(Levitzki，N.)、赫爾司亭(Herstein，I.N.)也相繼證明這一結論。

基本介紹

• 中文名：詣零理想
• 外文名：Nil ideal
• 別名：詣零子環
• 所屬學科：數學
• 相關概念：環、理想、單位元、冪零理想等

定義

定義一

設 為任意一個環，如果 且有自然數n使 ，則說 是 的一個詣零元素，又當n是使 的最小自然數時，就說n是 的詣零指數，設L是 的一個左理想，如果L中元素都是詣零元素，則說L是 的一個詣零左理想；如果有自然數n使 ，則說L是 的一個冪零左理想。同理可定義詣零右理想與想詣零兩邊理以及冪零右理想與冪零兩邊理想。顯然，冪零左(右、兩邊)理想為特殊的詣零左(右、兩邊)理想，還可以定義詣零環、詣零子環、冪零環、冪零子環等，顯然理想的詣零性與冪零性均為環同態下的不變性。

定義二

若A是環R的理想，則一般僅有關係式 和 ，如果R有單位元，則必有RA=AR=A，所以我們常把R稱為單位理想，稱理想A為冪等理想，如果，因而必有 ， 稱理想A為冪零理想，如果存在自然數n使 (注意：未必有 )，易見，此時A中任意n個元素的乘積必為0，特別，A中任意元都是冪零元，任意元都是冪零元的理想稱為詣零理想。因此，冪零理想必是詣零理想，反之不然，例如，交換環中冪零元全體成詣零理想，但未必是冪零理想。

相關性質與定理

命題1 的兩個冪零左理想 與 之和 + 仍為冪零的。

命題2 如果L是 的一個冪零左理想，則 為 的冪零兩邊理想。

命題3

⑴如果L是 的冪零左理想，則 為 的冪零兩邊理想。

由定義易知 為 的兩邊理想(它是 的含L的最小兩邊理想），其冪零性可由命題1、2而知。此命題說明 的冪零左理想恆可擴大成為 的冪零兩邊理想。

⑵如果R是 的冪零右理想，則 為 的冪零兩邊理想。

命題4 任意環 的一切冪零左、右及兩邊理想的並集N是 的一個詣零兩邊理想。

命題5 的兩個詣零兩邊理想A，B之和A+B仍為詣零的。

命題6 含有非0的詣零左理想等價於 含有非0的詣零右理想。

命題7 任意環 的一個子環S為詣零的必要而且只要有 的詣零兩邊理想M使S在自然同態映射

下的映象 為詣零的。

命題8 如果S為 的詣零子環，M為 的詣零兩邊理想。則 (即所有 作成的子集， )為 的詣零子環。

對於冪零性同樣有：

命題9 的子環S為冪零的 有 的冪零兩邊理想M使S在( )下的映象 為冪零的。

命題10 如果S與M分別是 的冪零子環與冪零兩邊理想，則 為 的冪零子環。

定理1 的上指數為n的左(右)理想( )恆含有 的上指數為3或2的左(右)理想。

定理2 的上指數為3的左理想L必含有 的上指數為2的左理想。

定理3 中上指數為2的左理想L恆為 的若干個冪零指數為2的冪零左理想的並集。