基本介紹
- 中文名：葛立恆掃描法
- 外文名：Graham's scan
- 分類：數理科學
算法步驟與圖解,時間複雜度,偽代碼,
算法步驟與圖解
第一步：找到最下邊的點，如果有多個點縱坐標相同的點都在最下方，則選取最左邊的。在右圖中這個點是P。這一步只需要掃描一遍所有的點即可，時間複雜度為
。
第二步：將所有的點按照相對於第一步中的得到的點P的極角大小進行排序。注意這一步並不需要真的通過計算反三角函式來獲取與x軸夾角的大小。可以直接使用該點與P點連線的斜率，或者由P點到該點向量的與沿x軸單位向量的點積來減少計算量。可以使用諸如快速排序、堆排序之類的算法進行排序，時間複雜度為
。
第三步：維護一個棧，以保存當前的凸包。按第二步中排序得到的結果，依次將點加入到棧中，如果正在考慮的點與棧頂的兩個點不是“向左轉”的，就表明當前棧頂的點並不在凸包上，而我們需要將其彈出棧，重複這一個過程直到正在考慮的點與棧頂的兩個點是“向左轉”的。右邊的圖解給出了“向左轉”和“向右轉”的示意：
- 剛開始的兩個點P、A直接入棧。
- 在點B加入時，P->A->B就構成左轉，因此直接加入點B即可。
- 接下來加入點C，A->B->C還是構成左轉，因此直接加入點C。
- 繼續加入點D時，B->C->D就變成右轉了，此時可以觀察到如果將BD連線，C將被包含在多邊形的內部，因此點C出棧。注意需要繼續檢查A->B->D是左轉還是右轉，如果還是右轉的話B點需要繼續出棧，以此類推。這個例子比較簡單，A->B->D已經是左轉了，D點可以入棧。
- 最後回到P點，B->D->P是左轉，算法完成，所求凸包為四邊形PABD。
另外，如果發現三點共線的情況，算法可以考慮將其視為左轉或者右轉。這取決於究竟只是要求凸包的邊界，還是要找到在凸包邊界上所有的點。
我們需要簡單地計算兩個向量的有向面積，即兩個向量的叉乘的結果來判斷兩個向量的相對位置。
假設三個點分別是
，則它們的有向面積為 
。如果其結果為0，這三個點是共線的；如果其結果為正，這三個點是向左轉的；如果其結果為負，則它們是向右轉的。
時間複雜度
排序的複雜度為
。儘管它的主循環看起來是
的時間複雜度，但由於每個點要多次在棧中查找若且唯若其相對與棧頂的點是“向右轉”的，這個過程實際上是
的時間複雜度，並且每一個點至多被考慮兩次，而每個點只在點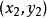
產生一個“向左轉”時被訪問一次（因為算法進行到點
之後，點
由於產生了一個“右轉”而被刪去），因此，總的時間複雜度由排序時間決定，即
。
偽代碼
定義：
# 當ccw函式的值為正的時候，三個點為“左轉”（counter-clockwise turn），如果是負的，則是“右轉”的，而如果 # 為0，則三點共線，因為ccw函式計算了由p1,p2,p3三個點圍成的三角形的有向面積 function ccw(p1, p2, p3): return (p2.x - p1.x)*(p3.y - p1.y) - (p2.y - p1.y)*(p3.x - p1.x)
然後結果存在points數組內：
let N = number of points let points[N+1] = the array of points swap points[1] with the point with the lowest y-coordinate sort points by polar angle with points[1] # points[0] 是結束循環的標記點 let points[0] = points[N] # M 是圍成凸包的點的個數 let M = 1 for i = 2 to N: # Find next valid point on convex hull. while ccw(points[M-1], points[M], points[i]) <= 0: if M > 1: M -= 1 # All points are collinear else if i == N: break else i += 1 # 更新M，並把points[i]放到正確的位置 M += 1 swap points[M] with points[i]
