基本介紹
- 中文名:艾里函式
- 外文名:airy function
- 表達式:Ai(x)=1/π*∫cos(t^3/3+xt) dt (0~+∞)
- 提出者:喬治·比德爾·艾里
- 提出時間:1838
- 套用學科:數學
概念介紹
定義
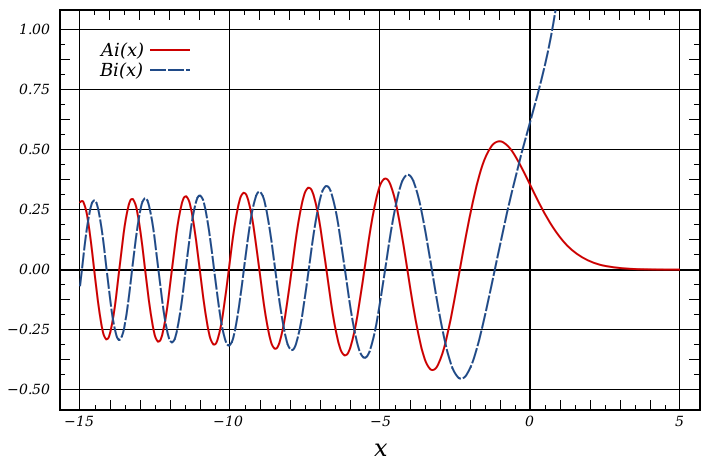 艾里函式圖像
艾里函式圖像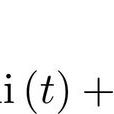
 艾里函式圖像
艾里函式圖像英文名 airy function。英國英格蘭天文學家、數學家喬治·比德爾·艾里命名的特殊函式,他在1838年研究光學的時候遇到了這個函式。Ai(x)的記法是Harold Jeffreys引進...
這個方程稱為艾里方程或斯托克斯方程。這是最簡單的二階線性微分方程,它有一個轉折點,在這一點函式由周期性的振動轉變為指數增長(或衰減)。...
廣義艾里函式(GeneralizedAiryFunctions)是艾里函式的推廣,是廣義艾里方程的解w_zz=z^nw。...
Φ(z)和Ψ(z)稱為科洛索夫函式或穆斯赫利什維利函式,也稱為艾里函式。 [1] 科洛索夫函式解析函式邊值問題 編輯 解析函式邊值問題是指求某些區域中的解析...
喬治·比德爾·艾里(1801年7月27日-1892年1月2日)英國第七任皇家天文學家(1835~1881)。曾為皇家格林威治天文台安裝新的設備,使數千次觀察記錄免遭埋沒。但...
艾里函式Ai(x)是微分方程y“-xy=0的解;它在物理學中有很多套用。 [3] 漸近分析套用 編輯 漸近分析方法在多個科學領域得到套用。在統計,漸近理論提供限制的近...
附錄A艾里函式A 1艾里微分方程A 2艾里函式的零點附錄B遠場表達式B 1二維的情形B 1 1遠場公式B 1 2近場/遠場變換B 1 3收發分置的RCSB 2三維的情形...
弗蘭之-克爾德什效應的原來構想是波函式‘流入”帶gab的結果;加電場時,電子和空穴的波函式從平面波變為艾里(Airy)函式,艾里函式有一“尾”。它延伸到經典的禁帶...
如求特殊函式值、隨機數、排序、最最佳化、快速傅立葉變換、譜分析、小波變換、...6.7 深入討論:分數階貝塞爾函式、艾里函式、球面貝塞爾函式 6.8 球面調和函式...
b 艾里函式c 勒讓德多項式d 合流超幾何函式e 超幾何函式 f 含有合流超幾何函式的積分計算 索引 [1] 參考資料 1. 0 [引用日期2018-06-03] ...
