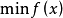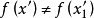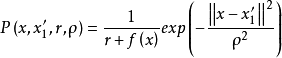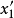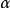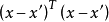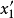確定性算法是利用問題的解析性質，產生一確定的有限或無限點序列使其收斂於全局最優解。這類方法依據某一確定性策略搜尋局部極小，並試圖跳躍已獲得的局部極小而達到某個全局最優點，能充分利用問題的解析性質，從而計算效率高。如填充函式法、打洞函式法、D.C.規划算法、區間法、單調規劃、分支定界方法和積分水平集方法等，這些算法的構造都涉及到已知目標函式的某些局部性質或者全局性質。其中，函式的連續性、可微性認為是局部性質，而凸性、單調性、稠密性、等度連續性、李普希茲連續、水平集等通常稱為全局性的解析性質。
基本介紹
- 中文名：確定性算法
- 外文名：deterministic algorithm
- 套用：全局最最佳化問題
- 特點：計算效率高
- 常用算法：填充函式法、打洞函式法等
- 相關算法：隨機性算法
全局最佳化問題,填充函式法,打洞函式法,D.C.規划算法,區間方法,分支定界方法,
全局最佳化問題
全局最佳化問題的一般形式是：
其中，
是可行域，
是目標函式。上述問題一般稱為原問題，這裡記為問題(1)。根據可行域X的不同情況，問題(1)又可分為多種類型。如果X=
，則得無約束全局最佳化問題，記為問題(2)；如果X={ |
}為一個閉箱，則得閉箱約束全局最佳化問題，記為問題(3)；如果X是一個多面體，則得線性約束全局最佳化問題。
填充函式法
填充函式是由西安交通大學的R.Ge(葛仁溥)教授首先提出的，填充函式法充分地利用了函式在可行域上的局部性質。
填充函式的定義如下：
函式p(x，
)稱為f(x)在局部極小點 處的填充函式，如果滿足：
(1) 是p(x， )的一個嚴格局部極大點，f(x)在點 處的盆谷
成為p(x， )的峰的一部分；
(2) p(x， )在比
高的盆谷里沒有平穩點；
(3) 如果存在比
低的盆谷
，則存在x'∈ 主使得p(x， )在x'和 的連線上存在極小點．
由填充函式的定義可以看出，如果當前極小點不是全局極小點的話，通過極小化填充函式則可以跳出原問題當前局部極小點，併到達一個原問題函式值比當前局部極小值還要小的點。因此，從該點出發極小化原問題目標函式，必將導致一個原問題目標函式值更小的局部極小點。
填充函式算法由兩個階段組成：極小化階段和填充階段。這兩個階段交替使用直到找不到更好的局部極小點。在第一階段里，可以用經典的極小化算法尋找目標函式的一個局部極小值點
。然後進入第二階段，在當前極小點 處定義一個填充函式，通過極小化填充函式，找到點
，使得
，而後以x'為初始點，重複第一步，一直到找不到更好的局部極小點。為此葛仁溥給出了一個兩個參數的填充函式函式：
填充函式的優點是較多地利用了函式的性質，所以收斂速度比較快，算法的設計和執行也相對容易；缺點是填充函式過多依賴一些未知參數，這就增加了算法設計之前的工作量，要經大量的實驗，來確定參數的取值範圍，以確保能找到滿意的全局最優解，而且填充函式利用的是線搜尋，所以對尋找低盆谷的點也有很大的難度。
打洞函式法
打洞函式法是由Levy和Montalvo在1985年首先提出的，它由一系列循環組成，每個循環包括兩個階段：局部極小化階段和打洞階段。
首先是極小化階段，由一個初始點出發，套用局部極小化算法，求得f(x)的一局部極小點
。其次是打洞階段，先定義 處的打洞函式：
這裡
是
的強度，然後尋找T(x， )≤0的點，即找到
，使
，由x'作為初始點開始下一輪循環，必將得到一個更好的極小點。
採用適當極小化打洞函式的方法找到一個局部極小點x'，並對其進行討論：
(1) 如果x'=
，則增大
，使得x'不再是T(x， )的局部極小點。
(2) 如果x'≠ ：並且
，那么構造新的打洞函式：
這裡，
是
的強度，目的是使x'不再是T(x，
)的局部極小點，防止極小化T(x，
)時又得到x'，然後重新極小化T(x，
)。
(3) 如果f(x')≤f(
)，則由x'為初始點開始下一輪循環。
打洞函式存在下述缺陷：
(1) 極的強度
與問題有關，當 增大到足夠大時算法才會有效，而增加 ，算法必須重新開始，從而增加工作量。
(2) 打洞函式可能找到另一局部極小點x'，成立f(x')≥f(
)。這樣對於第二個局部極小點x'，必須加上另一個極，打洞過程又要重新開始，又增加了工作量。
(3) 極的增加會引起打洞函式成為平坦，這時候極小點很難求。
D.C.規划算法
通過引入變數t，下面的D.C.規劃問題：
可以轉化為等價的凹極小化問題（記為問題(4)）：
顯然，目標函式
是凹的，可行域
是一個凸集，因此，如果(x‘，t‘)是問題(4)的一個全局最優解，則x’是D.C.規劃問題的一個全局最優解，且t‘=f(x‘)。
因此，對於任一D.C.規劃問題都可以通過凹極小化算法求解。對於凹極小化問題，人們已經提出了一些算法，這些算法多以分枝定界技巧、割平面方法、最優性條件和整數規劃等方法為基礎，且它們的有效性依賴於所要解決問題的結構特點。
區間方法
區間方法考慮的是問題(2)，其基本思想是以區間分析為基礎，按照區間算術運算規則用區間變數代替點變數進行區間計算，並將分支定界法和Moore-Skelboe算法等方法相結合。對這類算法，Moore首次提出區間全局最佳化這一概念。在這一研究領域裡，所有的算法都包含精確區間計算，以及算法的執行效率依賴於目標函式、梯度和約束區間擴張的構造方法。這類方法一般分為五個基本步驟：定界、分支、終止、刪除和分裂。其中包括區間分裂規則、刪除規則及區間選擇規則，不同的區間算法在於這幾種規則的不同處理手段上。
區間方法和其他方法(即以點搜尋方式產生近似點序列)相比，它的突出優點是對於低維空間中全局最佳化問題，能在給定精度內求出問題的全部全局極小點。特別地，對於二維空間中的單變數目標函式，建立了計算效率很高的求一元函式全局極小的區間斜率算法。缺點是當用於高維全局最佳化問題時，算法的計算量很大，對於區間分裂規則、刪除規則及區間選擇規則以及它們的檢驗條件的確定，難度都很大。
分支定界方法
在分支定界算法中，可行域得到鬆弛，並且把原區域逐次分割成越來越多的小區域，這個過程稱為分支；在這些小區域內，確定目標函式的下界和上界，這個過程稱為定界。在算法的某個階段，對於在其內下界大於當前最小的上界的小區域，將其刪除，這個過程稱為剪支，因為這些小區域中顯然不包含最優解。隨著分支越來越細，最小上界的不斷下降，最大下界的不斷上升，當最大下界和最小上界之差趨於零，同時細分的小區域收縮為一個點時，我們可以得到目標函式的全局極小值和全局極小點。
各種分支定界算法在求解連續變數的全局最最佳化問題時，有如下共同的特點：
(1) 對目標函式和可行域有較高的要求，以便於分支和定界。算法的效率與分支和定界方法的效率緊密相關。
(2) 在算法實施時，需要儲存越來越多的細分的小區域和目標函式在其上的下界，這使得在編程時，對數據結構的選擇、計算機記憶體的使用提出了更高的要求。
