基本介紹
- 中文名：相對素數
- 對應：給定的整數
- 特點：大於等於2
- 屬性：整除的整數.
定義,相對素數特徵,周期性,密度,密度推導公式,排列組合的和,特素數殊,自然相對素數,特徵,
定義
相對素數指不能被所有給定的整數（不能為0）整除的整數.
例如：
相對於1的相對素數為
。
相對於2的相對素數為全體正奇數和負奇數。
相對於{2,3,4,5,6,7,8，……99,100}的相對素數為所有不能被2~100內整數整數整數整除的整數。
9是相對於{2,5,}的相對素數。
與素數的區別與聯繫
素數的的取值範圍為所有大於等於2的正整數，相對素數取值範圍為全體整數。
素數是相對於全體大於等於2的整數，相對素數是相對於不含0的整數集合。
素數可以被自身整除，即包含於其相對範圍；相對素數除例外規定外，不包含於其相對範圍，即“不能被自身整除”。
素數和相對素數度可以用篩法獲得。
相對素數特徵
周期性
相對於整數集C（不含0,1，-1）的相對素數呈現周期為整數集合C內所有整數積|B|的周期性。
例如：相對於{2,3,4,-5}的相對素數呈現周期為120的周期。
相對於{-4,6}的相對素數呈現周期為24的周期性。
最小周期
將C中所有元素取絕對值並用素數乘積代替，然後兩兩比較，消去共有的素因子一次，當一數消去共有素因子後得1，即另一數為其倍數，直接消去另一數，或表述為先消去為其他元素整數倍的元素。剩下的數再按照上述方法相乘，得數Q,則Q為相對於整數集合C的最小周期。可以表示為消去為其他元素整數倍的元素後剩下的元素的最小正公倍數，例如：
相對於C={2,3,4，-5}，最小周期為30
相對於C={-4， 6},最小周期為12
相對於C={2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20}最小周期=
=9699690
密度
由於相對有周期性，所以其密度等於周期內元素除以周期。例如：
相對於C={2}，周期為2，一個周期內有元素1個，密度為1
2=0.5
相對於C={2，3}，周期為6，一個周期內有元素2個，密度為26=
=
.其中稱為相對於C的真密度。
相對於C={2,3,4,},周期為6，一個周期內有元素2個，密度為26==.
相對於C={2,3,4,5},周期為30，一個周期內有元素8個，密度為830=
=
相對於C={2,3,4,5，6,7},周期為210，一個周期內有元素48個，密度為48210=
=
相對於C={2,3,4,5，6,7,8,9,10,11},周期為2310，一個周期內有元素480個，密度為
4802310=
=
……
密度推導公式
相對於C={P1，P2，P3，……Pn-1,Pn}的相對素數的密度為1-
P1*P2為P1,P2的最低公倍數，
表示
中都包含的你容，其他的同理。
由上面計算可知：
,
,
,
.滿足
若對於後面任意
，只要它前面的都滿足，則它也滿足，則恆成立。
將代入上式得
=
=
=
當n為奇數時，
對於任意一個k都有一個n- k與其對應，且
由上式可知，當n為偶數時，可以分解為兩個比n小1的奇數的排列組合的和。
當n為偶數時
=
=0
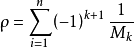
加入一個C中任意元素整數倍的元素，相對素數的密度不變，即
不變。
證明：
設B為C中任一元素A的整數倍，將C分為{A}和{A}在集合C上的補集M。則M有n-個元素。1用
表示M中k個元素的最低公倍數。相對於C的相對素數密度為1-，求將B增加入C中，密度的變化量。
將新元素代入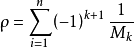得
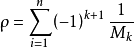
因為B為A的整數倍，所以B於A的最低公倍數為B,即B*A=B
注意，公式中所有公倍數全是正整數且為絕對值最小且不為0的最低公倍數。負數直接取正數運算。
B*A*=B*
將此關係代入上式得
即相對整數集合中任意元素的整數倍添加入相對整數集合後，相對素數密度不變。
排列組合的和
由
=知：
所以關於N的排列組合奇數項和偶數項的和想等且都為
特素數殊
自然相對素數
關於值域和相對域都為大於等於2的整數且相對域為初始數值為2且為連續整數，並且相對素數可以被自身整除（商為1，因為1不包含於大於等於2的整數，故不考慮）的相對素數
等同於篩法求素數，我們定義為自然相對素數。
設我們求關於[2,M]的自然相對素數，根據上面的結論，即相對整數集合中任意元素的整數倍添加入相對整數集合後，相對素數密度不變，和求最小相對素數周期線消去為其他元素整數倍的元素知：
關於[2，M]的相對素數最小周期為其中所有素數的最低公倍數，即為中所有素數的乘積。此相對素數等同於關於[2，M]中所有素數的相對素數。
關於[2,M]的自然相對素數等於關於[2,M]相對素數並上[2,M]內所有的素數。
根據素數驗證法知，關於[2,M]的自然相對素數，在值小於等於
的所有自然相對素數，全為素數。
特徵
一：關於[2,M]的自然相對素數等同於關於[2,M]內所有素數的相對素數並上[2,M]內所有的素數。
證明：設B為[2,M]中一個合數，則B必有素因子且素因子包含於[2,M]。
設A為B的一個素因子，則任何B的整數倍都是A的整數倍，設將B踢出[2,M]，相對素數無變化。
因為B為任意合元素，故所有合元素對[2,M]相對素數無影響，又關於[2,M]的自然相對素數包含[2,M]內所有的素數，關於[2,M]內所有素數的相對素數並不包含[2,M]內所有的素數，
故關於[2,M]的自然相對素數等同於關於[2,M]內所有素數的相對素數並上[2,M]內所有的素數。
二：用Pn表示[2,M]內所有素數，有關於[2,M]的自然相對素數的密度1-=
=
證明：關於{2,}的自然相對素數的密度為
，滿足上式；
關於{2,3}的自然相對素數的密度為
，滿足上式；
關於{2,3,4,5}的自然相對素數為
，滿足上式；
……
若任一素數有如果其前面所有的素數滿足上式，則其自身也滿足上式，則上式成立。
因為自然相對素數等同於相對於其中所有素數的相對素數和其中素數的並集，所有合數可以忽略。
設有任意素數P,其前面所有素數滿足上式，其對密度的影響為
其中Qn表示前面所有的素數中n個素數的最低公倍數，即他們的乘積，P*Qn表示P與n個前面素數的乘積。
簡化上式得
=
=
=
加入P後相對素數密度變為原來的
倍，即乘以
滿足上式要求。
故上式成立。
注意：此中密度不是真密度，只有取值為大於[2,M]內最大質數P且值域為周期整數倍是才是真密度。
存在素數“無人區“
設相對於[2,M]的相對素數，M取很大的數字。根據相對素數的性質可知，其存在一個周期Q為2至M內所有質數的乘積。則[Q+2,Q+M]內全為合數，且此區域呈現周期為Q的周期出現。即[KQ+2,KQ+M]
內所有整數都為合數。
證明略。
二：加常量的相對素數
表述為對相對域內整數去其整數倍加常量後所剩的數，常量對密度無影響。
自然相對素數證明素數有無限個
證明：
設素數是有限的，最大的素數為P,相對於[2,P]自然相對素數的周期為
其中N為素數個數，Pk表示第第k個素數。因為素數是有限的，所以存在一數Q為所有素數的積，則（P,P+Q]內有固定數目且不為0個的相對素數。取離P最近的一個Pn+1,若Pn+1小於P的平方，根據素數判定方法知，Pn+1為素數。則P不為最大素數。若Pn+1大於P的平方，因為P至其平方根內全是合數，所以其平方根內所有素數即為2至P內所有素數，按照素數判定法，其也為素數，即P不為最大素數。
所以，無最大素數。即素數有無限個。
哥德巴赫猜想的相對素數表述
對於任意大於等於2的整數N有2N為偶數，有2N的平方根內最大的整數Q，用N對[2,Q]內所有數做如下篩法：
值域在[2,N]內。對[2,Q]內任意數都做如下篩除，取[2,Q]內任意數M，N=MA+Z A為整數，Z為小於M大於等於0的整數，即為餘數。對值域內所有數做如下篩除，M的除其自身的整數倍和M的整數倍減去。即篩去MK（K不為1）和MK-Z（N=2且M=2時，K不為1）
即N=2時，M=2，Z=0 ，K不為1,所以2不被篩除，有4=2+2
其他情況K都可以取值1
N不為2時：
Z=0,篩去MK K所有整數
Z不為0時，篩去MK K不為1 再篩去MK+2Z
在值域[2,N]中剩餘的數H有H和2N-H都為素數，即滿足哥德巴赫猜想的要求。
若存在一個N,使用上述篩法篩除後，在其值域[2,N]內所有元素都被篩除，即不滿足哥德巴赫猜想要求，則哥德巴赫猜想不成立。
相對素數存在周期和密度。
上述篩法值域在整數上拓展後密度為
P為[2,Q]內不為2的任意素數，若N為P的倍取1，則P表示為P1.N不為P的整數倍取2，P表述為P2.
密度1-
=
大於0
其在[2,Q]上不為真密度。
