基本介紹
- 中文名:特徵子空間
- 外文名:characteristic subspace
- 所屬學科:數理科學
- 屬性:線性變換的一特徵值的子空間
定義
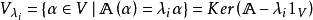

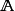
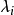

對角化條件

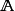

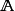




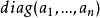


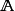

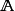
幾何重數與代數重數

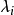
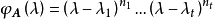
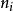

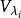
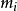
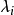
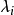


例題分析與解答




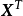


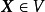

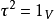


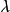

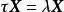
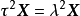







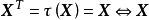


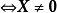




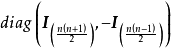
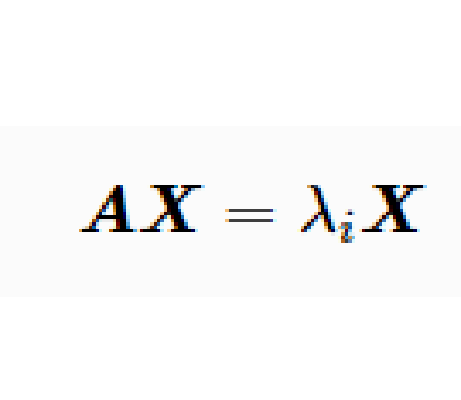
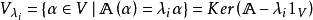

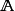
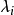


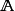

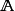




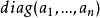


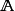

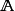

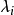
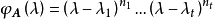
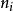

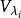
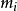
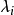
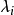






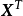


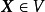

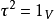


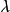

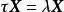
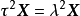







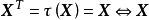


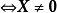




特徵子空間(characteristic subspace)是一類重要的子空間,即對應於線性變換的一特徵值的子空間。設V是域P上的線性空間,σ是V的一個線性變換,σ的對應於特徵值λ...
聚類分析是數據挖掘領域中的關鍵技術之一。高維數據聚類是聚類分析技術的難點和重點,子空間聚類是實現高維數據集聚類的有效途徑,它是在高維數據空間中對傳統聚類...
在遷移學習中,基於特徵映射方法是把各個領域的數據從原始高維特徵空間映射到低維特徵空間,在該低維空間下,源領域數據與目標領域數據擁有相同的分布。這樣就可以利用...
子空間聚類分析是數據挖掘領域中的關鍵技術之一,它是在高維數據空間中對傳統聚類算法的一種擴展,其思想是將搜尋局部化在相關維中進行。...
韓正之在學術上的主要成就是:定義及全面研究了線性系統(A,B)特徵子空間理論,並成功用於大系統分散控制的設計。建立非線性系統分離設計研究。首次給出一個例子說明...
子空間的形式很多,有生成子空間、值域空間、零空間和特徵子空間等等,我們重點看看特徵子空間。一個空間可以劃分為若干個特徵子空間的直和形式,而每個特徵子空間的...
3.2 特徵空間穩健波束形成算法 443.2.1 主分量波束形成算法 443.2.2 投影波束形成算法 453.2.3 互譜特徵子空間波束形成算法 46...
子空間聚類算法拓展了特徵選擇的任務,嘗試在相同數據集的不同子空間上發現聚類。和特徵選擇一樣,子空間聚類需要使用一種搜尋策略和評測標準來篩選出需要聚類的簇,...
本文對掌紋識別技術的國內外研究現狀作簡單介紹。下面分別介紹基於掌紋的點特徵與線特徵、紋理特徵、子空間分析和分級特徵融合的掌紋識別算法。...
的特徵值。② 為正規矩陣,則與 酉相似的矩陣都是正規矩陣;③ 為正規矩陣,則 必有 個線性無關的特徵向量;④ 為正規矩陣,則 的屬於不同特徵值的特徵子空間是...
