基本介紹
- 中文名:牛頓法
- 外文名:Newton's method
- 提出者:艾薩克·牛頓
- 提出時間:1736年
- 出自:Method of Fluxions
- 又稱:牛頓-拉弗森方法
- 套用學科:數學
起源
原理
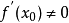
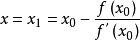
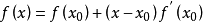
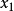

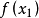

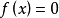
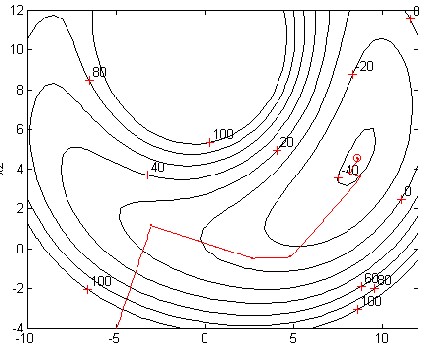 搜尋方向較近似於牛頓法
搜尋方向較近似於牛頓法
 | 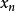 |
0 | 1.5 |
1 | 1.7371 |
2 | 1.6987 |
3 | 1.6975 |
... | ... |
切線法
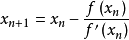
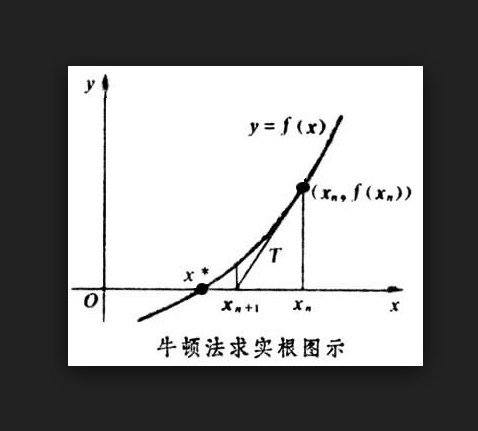
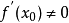
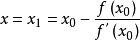
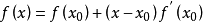
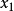

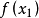

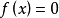
 搜尋方向較近似於牛頓法
搜尋方向較近似於牛頓法
 | 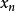 |
0 | 1.5 |
1 | 1.7371 |
2 | 1.6987 |
3 | 1.6975 |
... | ... |
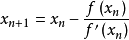
牛頓疊代法(Newton's method)又稱為牛頓-拉夫遜(拉弗森)方法(Newton-Raphson method),它是牛頓在17世紀提出的一種在實數域和複數域上近似求解方程的方法。...
牛頓法最初由艾薩克·牛頓於1736年在 Method of Fluxions 中公開提出。而事實上方法此時已經由Joseph Raphson於1690年在Analysis Aequationum中提出,與牛頓法相關的...
牛頓逼近法-牛頓逼近法是牛頓在17世紀提出的一種在實數域和複數域上近似求解方程的方法。多數方程不存在求根公式,因此求精確根非常困難,甚至不可能,從而尋找方程的...
高斯—牛頓疊代法的基本思想是使用泰勒級數展開式去近似地代替非線性回歸模型,然後通過多次疊代,多次修正回歸係數,使回歸係數不斷逼近非線性回歸模型的最佳回歸係數,...
高斯一牛頓疊代法(Gauss-Newton iteration method)是非線性回歸模型中求回歸參數進行最小二乘的一種疊代方法,該法使用泰勒級數展開式去近似地代替非線性回歸模型,...
(非線性方程組的)牛頓(解)法(Newton meth-od (of nonlinear equations ))解非線性方程組的一種經典方法,它是方程求根牛頓法的推廣。...
艾薩克·牛頓(1643年1月4日—1727年3月31日)爵士,英國皇家學會會長,英國著名的物理學家,百科全書式的“全才”,著有《自然哲學的數學原理》、《光學》。他在...
《非線性問題的牛頓法——仿射不變性和自適應算法》是2006年1月科學出版社出版的圖書,作者是Peter,D。...
非線性問題的牛頓法——仿射不變性和自適應算法 Newton Methods for Nonlinear Problems Affine and Adaptive Algorithms 國外數學名著系列(影印版) -15[德]Peter,D...
DFP算法(Davidon-Fletcher-Powell algorithm)一種秩2擬牛頓法,是由Davidon,Fletcher,Powell三個人的名字的首字母命名的,是求解非線性最佳化問題最有效的方法之一。...
疊代法也稱輾轉法,是一種不斷用變數的舊值遞推新值的過程,跟疊代法相對應的是直接法(或者稱為一次解法),即一次性解決問題。疊代算法是用計算機解決問題的一種...
然而,對於多項式,存在特定的使用代數學性質以定位根的所在區間(或復根所在的圓盤)的算法,這個區間(或圓盤)足夠小以能保證數值算法(例如牛頓法)能收斂到唯一被定位...
BFGS法(BFGS method)是一種擬牛頓法,指用BFGS矩陣作為擬牛頓法中的對稱正定疊代矩陣的方法,此法是1970年前後由柏蘿登(C.G.Broyden)、弗萊徹(R.Fletcher)、戈德...
