混合常態分配

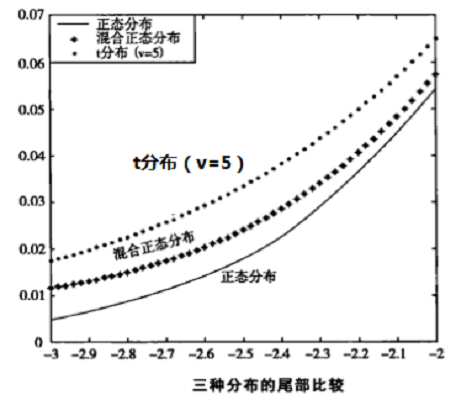
混合常態分配( mixture of normal distribution)具有厚尾。該模型認為對數收益率服從這樣一個過程：dlogS(t)=μdt+σg(t)dW，μ和σ是單個交易的均值和方差，W是標準布朗運動。當g(t) 是常數時，此模型變成標準的幾何布朗運動。 g(t) 是一個從屬隨機的過程，它刻畫了市場的交易活動時間。如果g(t) 被假定為對數常態分配，該混合過程也被稱為正態-對數正態混合。它的機率密度函式由Clark (1973)給出。

混合常態分配的關鍵是從屬過程的概念。Clark(1973)假設交易量是價格波動的原因，以及交易量就是那個從屬過程。假定個別交易是常態分配以及交易量是有限的，他證明混合常態分配具有厚尾。

混合常態分配直觀的優勢在於它直接與市場微觀結構有關，如信息流、交易量和交易次數。在一般情況下，混合常態分配不服從時間縮放。一些混合常態分配可以描述波動集群。

基本介紹

• 中文名：混合常態分配
• 外文名：mixture of normal distribution
• 所屬學科：數學
• 相關概念：厚尾、常態分配、混合分布等
• 別名：高斯混合分布 

定義

隨機變數X服從混合分布，則其密度函式為：

其中， 。 分別表示第 個分布的密度函式、均值和方差，且 相互獨立。若 表示常態分配時，則稱X服從一個由m個常態分配分量組成的混合常態分配。

在實際套用中，一個複雜的分布通常用兩個或三個常態分配分量經混合便可得到較好的逼近，能較好地描繪厚尾特徵(見圖1)。Tucker(1992)指出，在混合常態分配集中，由兩個常態分配組成的混合常態分配具有最好的描述性質：它們在將模型的參數個數減少到最小的程度下，提供了足夠的靈活性。

由定義可知服從一元混合常態分配的隨機變數 的密度函式為：

其中， , 為常態分配密度函式，記為 ，從密度函式形式上來看，混合常態分配具有常態分配的一些特性。

顯然當 或 時，上述混合分布便是一個常態分配。

同樣可知服從多元混合常態分配隨機變數 的密度函式為：

其中， 為多元常態分配密度函式， 為 維均值向量， 為 維協方差矩陣。

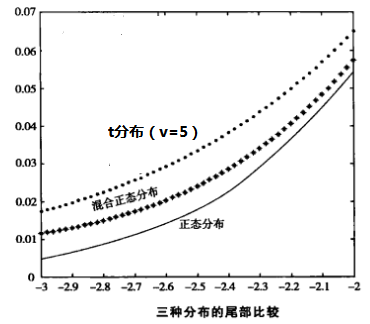圖1

混合常態分配的數字特徵

假定隨機變數 ，且各階矩都存在，則可求得前幾階矩為：

一階矩(均值) ：

二階矩：

方差：

三階矩：

四階矩：

由此可以計算出混合常態分配的偏度與峰度，為了簡便運算先設定：

則偏度為：

峰度為：

可得以下推論：

推論1

如果 ， 即 ， 則 。

可知該混合分布為對稱分布且具有厚尾特徵，若 給定， 是 嚴格減函式，在 嚴格增函式，在 上的凸函式，在 上的凹函式。

推論2

如果 即 ，則 ， 。

如果兩個常態分配分量具有相等的方差，即當 時，兩混合分布的權重係數相等時，具有薄尾特徵；當 時，則分布為不對稱分布，且當0.2113< <0.7887時，則分布為薄尾分布，當 ≤0.2113或 ≥0.7887時，則分布表現為厚尾分布。