基本介紹
- 中文名:模曲線
- 外文名:Modular curve
- 學科:數學
- 屬性:緊黎曼曲面
- 適用範圍:代數幾何及數論領域
- 相關名詞:李曼表面
簡介,分析定義,緊模曲線,舉例,型,
簡介
在數論和代數幾何中,模曲線 是黎曼表面或相關的代數曲線,通過積分2×2矩陣
是黎曼表面或相關的代數曲線,通過積分2×2矩陣 的模組化組的子群
的模組化組的子群 ,構造為復上半平面H的商。模曲線也可以用於指壓縮模曲線
,構造為復上半平面H的商。模曲線也可以用於指壓縮模曲線 ,它們是通過將有限多個點(稱為
,它們是通過將有限多個點(稱為 的尖點)添加到該商(通過在擴展的復上半平面上)而獲得的緊湊化。模曲線的參數以及
的尖點)添加到該商(通過在擴展的復上半平面上)而獲得的緊湊化。模曲線的參數以及 群的一些附加特徵擬合橢圓曲線的同構類。這個解釋給出了模曲線的純代數而不考慮複數的定義,而且證明了模曲線是在有理場Q上建立的,或者是一個循環場。後一種和它的概括在數論中是根本的重要性。
群的一些附加特徵擬合橢圓曲線的同構類。這個解釋給出了模曲線的純代數而不考慮複數的定義,而且證明了模曲線是在有理場Q上建立的,或者是一個循環場。後一種和它的概括在數論中是根本的重要性。






分析定義
模組化組 通過分數線性變換作用在上半平面上。 模曲線的分析定義涉及對於某些正整數N,
通過分數線性變換作用在上半平面上。 模曲線的分析定義涉及對於某些正整數N, 的同餘子群
的同餘子群 ,即包含
,即包含 的同餘子群,其中
的同餘子群,其中





緊模曲線
(1)H的任何開放子集;
(2)對於所有r> 0,集合 ;
;

(3)對於所有互質整數a,c和所有r> 0, 的像
的像


m,n是整數,並且

這使得 變成作為黎曼球
變成作為黎曼球 的子集的拓撲空間。 組
的子集的拓撲空間。 組 作用於子集
作用於子集 ,將其分解成有限的許多軌道,稱為
,將其分解成有限的許多軌道,稱為 的尖點。 如果
的尖點。 如果 在
在 上過渡運行,則空間
上過渡運行,則空間 \
\ 成為
成為 \H的Alexandroff壓縮。 再次,複數結構可以放在商
\H的Alexandroff壓縮。 再次,複數結構可以放在商 \
\ 上,使其變為表示為
上,使其變為表示為 的黎曼表面,其現在是緊湊的。 這個空間是
的黎曼表面,其現在是緊湊的。 這個空間是 的緊湊化。
的緊湊化。














舉例
最常見的示例是與子組 ,
, 和
和 相關聯的曲線
相關聯的曲線 ,
, 和
和 。
。






模曲線 具有屬性0:它是具有12個尖點的黎曼球,位於常規二十面體的頂點。 X(5)→X(1)通過二次面組在黎曼球體上來實現。 這個組是一個和A5和PSL(2,5)同構的簡單組。
具有屬性0:它是具有12個尖點的黎曼球,位於常規二十面體的頂點。 X(5)→X(1)通過二次面組在黎曼球體上來實現。 這個組是一個和A5和PSL(2,5)同構的簡單組。

模曲線 是具有24個尖點的3類克萊恩。 它可以解釋為具有三個柄的表面,由24個七邊形平鋪,每個面的中心具有尖點。 這些可以通過dessins d'enfants和Belyi函式來理解,而邊緣的頂點和中心(黑色和白色點)是0和1之間的點。X(7)→X(1)的伽羅瓦組是與PSL同構的一個168類的簡單組PSL(2,7)。
是具有24個尖點的3類克萊恩。 它可以解釋為具有三個柄的表面,由24個七邊形平鋪,每個面的中心具有尖點。 這些可以通過dessins d'enfants和Belyi函式來理解,而邊緣的頂點和中心(黑色和白色點)是0和1之間的點。X(7)→X(1)的伽羅瓦組是與PSL同構的一個168類的簡單組PSL(2,7)。

對於經典模曲線, 有一個明確的經典模型,有時被稱為模曲線。
有一個明確的經典模型,有時被稱為模曲線。 的定義可以重述如下:它是作為縮減模N的核心的模組組的子組。然後
的定義可以重述如下:它是作為縮減模N的核心的模組組的子組。然後 是上三角模N的矩陣的較大子組:
是上三角模N的矩陣的較大子組:





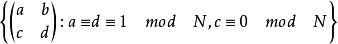
這些曲線具有作為具有水平結構的橢圓曲線的模數空間,並且因此它們在算術幾何中起重要作用。 水平為N的模曲線 是橢圓曲線的模空間。 對於
是橢圓曲線的模空間。 對於 和
和 ,層次結構分別是階數N和階N的循環子組。這些曲線已經被非常詳細地研究,特別是已知
,層次結構分別是階數N和階N的循環子組。這些曲線已經被非常詳細地研究,特別是已知 可以通過Q定義。
可以通過Q定義。




定義模曲線的方程是模方程式中最著名的例子。 “最佳模型”可以與直接從橢圓函式理論得出的結果不同。黑克操作員可以在幾何學上進行研究,作為連線成對的模曲線的對應關係。
型
X(N)→X(1)是伽羅瓦,伽羅瓦組SL(2,N)/ {1,-1},如果N為素數則等於PSL(2,N)。 套用黎曼 - 赫爾維茨公式和高斯 - 博內定理,可以計算 的屬。 對於素數級≥5,
的屬。 對於素數級≥5,


其中 是歐拉特徵,
是歐拉特徵, 是組PSL(2,p)的順序,
是組PSL(2,p)的順序, 是球(2,3,p)的角。 這產生一個公式
是球(2,3,p)的角。 這產生一個公式




因此,X(5)具有型0,X(7)具有型3,X(11)具有型26。對於p = 2或3,還必須考慮分支,即存在階數p PSL(2,Z)中的元素以及PSL(2,2)具有型6而不是型3的事實。對於涉及的任何級別N的模曲線X(N)的屬來說,存在更複雜的公式 N.的除數。

