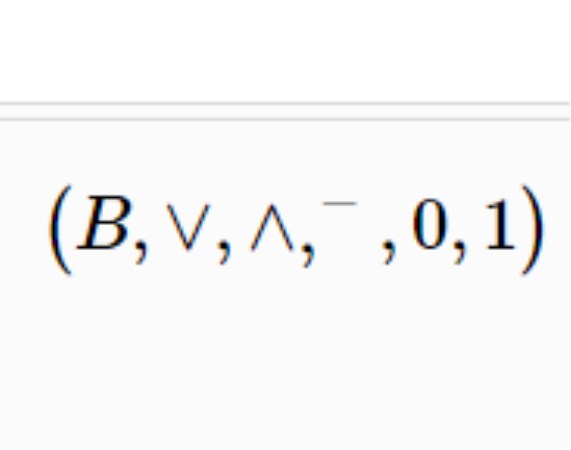有限布爾代數(finite Boolean algebra)是一種常用的布爾代數，指論域B是有限集的布爾代數。有限布爾代數的論域B的元素個數必是2的方冪2n(n=1，1，2，…)，n=0時的布爾代數是僅含一個元素的退化布爾代數，n=1時的布爾代數僅含0和1兩個元素，稱為二元布爾代數，區分有限與無限布爾代數是有意義的，因為有限布爾代數必是原子布爾代數，從而它同構於某個集A的所有子集構成的布爾代數；但一個無限布爾代數未必是一個原子布爾代數，故它無上述性質。
基本介紹
- 中文名：有限布爾代數
- 外文名：finite Boolean algebra
- 所屬學科：數學（布爾代數）
- 簡介：論域B是有限集的布爾代數
基本介紹,相關定理,
基本介紹
定義1 具有有限個元素的布爾代數稱為有限布爾代數。
對於有限布爾代數，有以下的結論：對於每一正整數n，必存在含有2n個元素的布爾代數；反之，任一有限布爾代數，它的元素個數必為2的冪次。元素個數相同的布爾代數都是同構的。
定義2 設
是一個布爾代數，a∈B且a≠0，若任意x∈B，有x∧a=a或x∧a=0， 則稱元素a為原子。
顯然原子是0的覆蓋，且若元素a覆蓋0，則a必是原子。
相關定理
定理1 設是一個布爾代數，a, b∈B是B的原子。若a≠b，則a∧b=0。
證明：假設a∧b≠0，由於a是原子，所以a∧b=b∧a=a。又b是原子，因此a∧b=b, 從而得到a=b，與已知條件a≠b矛盾。
定理2 設是一個有限布尓代數，任意b∈B，若b≠0，則至少存在一個原子a，使得a<b。
證明：如果b是原子，那麼由b
b得證。
如果b不是原子,那麼必存在b1使得0<b1<b。如果b1是原子，那么定理得證。否則,必存在b2使得0<b2<b1<b。
由於B有限,且有全下界0,故通過有限歩驟總可找到一個原子bi，使得
。它是
中的一條鏈，其中bi是原子，且bi<b。
定理3 設是一個有限布尓代數，任意b∈B，b≠0，令T(b)=
是B中所有小於等於b的原子構成的集合，則
，稱這個表示式為a的原子表示,且是唯一的表示，這裡的唯一性是指:若
，則有
定理4 ( Stone表示定理)設是一個有限布爾代數，S是B中的所有原子的集合，則和S的冪集代數(P(S),∪，∩，~，∅，S)同構。
由定理4可得如下推論:
推論1 有限布爾代數的元素個數必定等於 2n，其中n是該布爾代數中所有原子的個數。
推論2 任何一個具有2n個元素的有限布爾代數都是同構的。
