最短路問題（short-path problem）是網路理論解決的典型問題之一，可用來解決管路鋪設、線路安裝、廠區布局和設備更新等實際問題。基本內容是：若網路中的每條邊都有一個數值（長度、成本、時間等），則找出兩節點（通常是源節點和阱節點）之間總權和最小的路徑就是最短路問題。
基本介紹
- 中文名：最短路問題
- 外文名：short-path problem
- 解決算法：Floyd-Warshall等算法
- 實現方式：廣度優先搜尋、深度優先搜尋
- 範疇：圖論理論
- 套用領域：城市網路、艦船通道
理論概要,理論重點,單源最短路徑,全局最短路徑,兩點最短路徑,套用領域,城市網路,艦船通道,其他套用,套用算法,關於最短路問題的一個雙目標最佳化問題,求解最短路問題的一種最佳化矩陣算法,最短路問題的Floyd算法的若干討論,
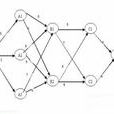
理論概要
最短路問題是圖論理論的一個經典問題。尋找最短路徑就是在指定網路中兩結點間找一條距離最小的路。最短路不僅僅指一般地理意義上的距離最短,還可以引申到其它的度量,如時間、費用、線路容量等。
最短路徑算法的選擇與實現是通道路線設計的基礎,最短路徑算法是計算機科學與地理信息科學等領域的研究熱點,很多網路相關問題均可納入最短路徑問題的範疇之中。經典的圖論與不斷發展完善的計算機數據結構及算法的有效結合使得新的最短路徑算法不斷湧現。
對最短路問題的研究早在上個世紀60年代以前就卓有成效了,其中對賦權圖的有效算法是由荷蘭著名計算機專家E.W.Dijkstra在1959年首次提出的,該算法能夠解決兩指定點間的最短路,也可以求解圖G中一特定點到其它各頂點的最短路。後來海斯在Dijkstra算法的基礎之上提出了海斯算法。但這兩種算法都不能解決含有負權的圖的最短路問題。因此由Ford提出了Ford算法,它能有效地解決含有負權的最短路問題。
理論重點
單源最短路徑
包括確定起點的最短路徑問題，確定終點的最短路徑問題（與確定起點的問題相反，該問題是已知終結結點，求最短路徑的問題。在無向圖中該問題與確定起點的問題完全等同，在有向圖中該問題等同於把所有路徑方向反轉的確定起點的問題。） 。
求解單源最短路徑問題可以採用Dijkstra算法，時間複雜度為O(|V|^2)。Dijkstra算法可以使用斐波那契堆、配對堆等支持Decrease-Key操作的數據結構來進一步最佳化，最佳化後的時間複雜度為O(|E|+|V|log|V|)。
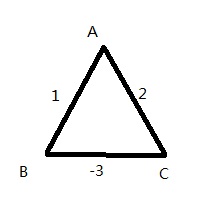
Dijkstra只可求無負權的最短路徑，因為其目光短淺，看不到後面可以消減的量。在正數中容易得證，若a<b，Dijkstra會取a，若再有一條路c，a+c<b+c是正確的。但引入負數後，可能會出現以下情況，Dijkstra會先選擇A-B這條邊，此時A->B的距離固定為1，不再改變，但其實A->B最短路是-1，雖然A->C的最短路是正確的，為-2，但這樣的算法是不可使用的。
如果圖中有負權迴路，可以採用Bellman-Ford算法，算法複雜度是O(|V||E|)。但Bellman-ford算法浪費了許多時間做無必要的鬆弛，可用SPFA算法進行最佳化，SPFA算法是用佇列進行的最佳化，最佳化後時間複雜度為O(k|E|)， 其中k為所有頂點進隊的平均次數，可以證明k一般小於等於2，由此可見該最佳化的效果十分顯著。
全局最短路徑
求圖中所有的最短路徑可以採用Floyd-Warshall算法，算法時間複雜度為O(|V|^3)。對於稀疏圖，還可採用Johnson算法，其採用Bellman-ford和Dijkstra作為其子函式，時間複雜度為O（VElgV）。二者都可計算含負權路徑的圖，但不可含有負環。
兩點最短路徑
套用領域
城市網路
運用最短路原理，解決交通運輸管理系統的問題，具有非常重要的現實意義。根據實時交通狀況，賦予城市路網中每段線路以時間權值，利用最短路原理，計算出車輛運行時間最短的路線並匯總，通過新媒體及時向廣大民眾發布信息，指導廣大民眾選擇行駛路線，進一步提高現有道路通行能力，提高道路服務水平，滿足現代化高速發展的需求。
艦船通道
利用圖論的經典理論和人群流量理論研究艦船人員通道路線的最佳化設計及最優線路選擇。對船舶通道進行路網抽象,建立網路圖,然後根據人群流動的相關理論,選取不同擁擠情況下的人員移動速度,從而確定各條路段(包括樓梯)的行程時間。以行程時間作為通道網路的路權，得出路阻矩陣以選擇一對起點/終點的最短時間路線為目標,建立最短路徑問題的數學模型,利用經典的Floyd算法確定最短路徑。將此方法套用於某艦艇多層甲板的通道網路中,計算結果並進行討論,最後在此研究的基礎上對通道設計相關問題的深化和拓展進行了探討和總結,並提出構想。
其他套用
火災救護，物流選址，網路空間建設等等，有著極為廣泛的套用。
套用算法
關於最短路問題的一個雙目標最佳化問題
本文研究了一個雙目標最短路問題的變形問題，在該變形問題中，一個目標函式還是路的長度，另一個目標函式則是路的容量。在Paretooptimal最優解的意義下，本文給出了一個時間複雜性為O(n3)的算法，在字典序最優解的意義下，本文給出了一個時間複雜性為O(n2)的算法。
對 (BsP )，在Pareto一optimal意義下,有時間複雜性為O(n3)的算法。
下面分析算法的時間複雜性,每循環一次至少刪去一個頂點,每次循環調用兩次Dijkstra算法，故算法的時間複雜性為O (n3)。
對(BsP)，在字典序意義下有時間複雜性為o(n2)的算法。
註：該算法在一定意義下是最好的，因為找一條：
→
的路的時間複雜性都為O(n2)。
求解最短路問題的一種最佳化矩陣算法
矩陣算法是求解不含負迴路的網路中所有頂點對之間最短路的有效算法之一，但當節點比較多時，計算的矩陣多，重複計算量大，降低了計算效率。為此，提出了一種最佳化的矩陣算法，該算法的思路是利用權矩陣計算網路任意兩節點之間的最短路長。計算實例表明，最佳化的矩陣算法減少了重複計算，簡化了路徑標註方法，提高了計算效率。
PSO 算法的早期收斂非常快，在算法初期應在保證粒子多樣性的基礎上，儘快讓算法進入局部搜尋，才能獲得更好的求解效率；而在算法後期則粒子應保留一定的搜尋能力，避免過早收斂。
最短路問題的Floyd算法的若干討論
對不含負迴路的網路中所有頂點對之間的最短路問題，通常採用Floyd算法。對此算法進行了討論，並對Floyd算法的計算過程作了一點改進。改進後的算法對階數不太大的網路進行較簡單的計算就能得出所有頂點對之間的最短路。
可以將問題分解，先找出最短的距離，然後在考慮如何找出對應的行進路線。如何找出最短路徑呢，這裡還是用到動態規劃的知識，對於任何一個城市而言，i到j的最短距離不外乎存在經過i與j之間的k和不經過k兩種可能，所以可以令k=1，2，3，...，n(n是城市的數目)，在檢查d(ij)與d(ik)+d(kj)的值；在此d(ik)與d(kj)分別是目前為止所知道的i到k與k到j的最短距離，因此d(ik)+d(kj)就是i到j經過k的最短距離。所以，若有d(ij)>d(ik)+d(kj)，就表示從i出發經過k再到j的距離要比原來的i到j距離短，自然把i到j的d(ij)重寫為d(ik)+d(kj)，每當一個k查完了，d(ij)就是目前的i到j的最短距離。重複這一過程，最後當查完所有的k時，d(ij)裡面存放的就是i到j之間的最短距離了。
