最優性,運籌學中的術語,對偶問題的基本性質之一。如果X是原問題的可行解,Y是對偶問題的可行解,並且CX=Yb,那么X和Y分別為原問題和對偶問題的最優解。這個定理說明了如果找到原問題和對偶問題的可行解,且它們目標函式值如果相等,那么這兩個可行解都是各自問題的最優解。
基本介紹
- 中文名:最優性
- 外文名:optimization condition
- 分類:數學 運籌學
- 形式:標準 矩陣
- 功能:找最優解
- 屬於:對偶問題
定義
標準形式
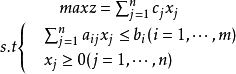


矩陣形式


數學證明
一般形式





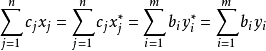

最優性,運籌學中的術語,對偶問題的基本性質之一。如果X是原問題的可行解,Y是對偶問題的可行解,並且CX=Yb,那么X和Y分別為原問題和對偶問題的最優解。這個定理說明了如果找到原問題和對偶問題的可行解,且它們目標函式值如果相等,那么這兩個可行解都是各自問題的最優解。
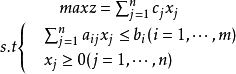









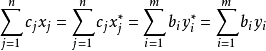
最優性,運籌學中的術語,對偶問題的基本性質之一。如果X是原問題的可行解,Y是對偶問題的可行解,並且CX=Yb,那么X和Y分別為原問題和對偶問題的最優解。這個定理...
最優性原理是指“多階段決策過程的最優決策序列具有這樣的性質:不論初始狀態和初始決策如何,對於前面決策所造成的某一狀態而言,其後各階段的決策序列必須構成最優...
《錐約束最佳化——最優性理論與增廣Lagrange方法》是2010年1月科學出版社出版的圖書,作者是張立衛。...
主要內容包括變分分析的相關基礎、約束集合的切錐與二階切集、對偶理論、非線性錐約束最佳化的一階最優性條件和二階最優性條件、三類重要的錐約束最佳化的最優性條件...
《最優控制:數學理論與智慧型方法(上冊)》是2017年09月出版的圖書,作者是張傑、王飛躍。...
研究在平穩隨機干擾下的回歸係數的最小二乘估計與最優估計之間的關係,首次證明了二乘估計具有瀵近最優性, 王壽仁為採用簡單的最小二乘估計提供理論。合作建立了我...
簡單的線性規劃指的是目標函式含兩個自變數的線性規劃,其最優解可以用數形結合方法求出。涉及更多個變數的線性規劃問題不能用初等方法解決。...
通過提供獨特的最優化特性,CUBRID可以支持更多的並發請求,更少的回響時間。...大容量和高擴展性 - 無限制的資料庫數量、表數量、以及表中行數量,任意大小的...
他給出了雙球信賴域子問題的最優性條件,證明了截斷共軛梯度法的“1/2 猜想” [21] 。袁亞湘在擬牛頓方法的理論研究方面,他和美國科學家合作證明了一類擬牛頓...
一、最優性條件 27二、疊代規則 28三、算法步驟 29四、單純形表 30第四節初始基可行解 33一、輔助規劃 34二、第一階段 34三、第二階段 36...
第3節動態規劃的最優性原理和最優性定理142 第4節動態規劃和靜態規劃的關係144 第5節動態規劃套用舉例151 習題171 參考資料174 四、 圖與網路分析 第...
8.1.2最優性原理及動態規劃的基本方法8.2動態規劃的模型建立與求解步驟8.2.1動態規劃的模型建立的基本要求8.2.2動態規劃的求解步驟8.2.3動態規劃的模型分類...
4.3.6新 BF 解的最優性檢驗 4.3.7第二次疊代和求得最優解 4.4單純形法的表格形式 4.4.1單純形法總結(以疊代1為例) 4.4.2最小比檢驗 4.4.3例題的第二...
《Re:從零開始的異世界廣播生活》獲得最優秀女性...(小林優役)的聲音出演所感動,從而產生了想要成為...《弱酸性百萬亞瑟王》第二型Refol 2017年 《機動戰士...
3.9.2 最優滾轉控制1583.9.3 多變數側航向控制:航向保持自動駕駛儀161...4.9.1 穩定性、可控性和可觀性216 4.9.2 跟蹤重力轉彎軌跡的標稱對象218 4.10...
4.5.3動態規劃的最優性定理、最最佳化原理 4.5.4多階段決策的動態規劃解法 4.5.5動態規劃的優點與缺點 第5章作戰兵力損耗理論 5.1基本概念 5.1.1總假設和記號...
哈密頓-雅可比-貝爾曼方程(Hamilton-Jacobi-Bellman equation,簡稱HJB方程)是一個偏微分方程,是最優控制的核心。HJB方程式的解是針對特定動態系統及相關代價函式下,有...
3.2.2 非線性控制律最優性討論3.2.3 一般情況下的線性化設計原理3.2.4 精確線性化的條件3.2.5 精確線性化的算法3.3 零動態設計原理與方法...
2.3.2 最大似然估計及其漸近統計最優性分析 392.3.3 加權最小二乘估計及其與最大似然估計的等價性 412.4 線性離散和連續時間系統中的若干預備知識 42...
6.1 霍夫曼編碼最優性的證明 796.2 低密度奇偶校驗碼(LDPC碼) 806.3 聯合高斯分布隨機變數 856.4 聯合高斯分布隨機變數的密度函式 86...
5.1動態規劃的最優性原理及其算法5.1.1求解多階段決策問題的方法5.1.2最最佳化原理和動態規劃遞推關係5.2動態規劃模型舉例5.2.1資源分配問題...
8.3.5 損失函式最優性8.4 習題8.5 雜錄8.5.1 單調功效函式8.5.2 似然比作為證據8.5.3 P-值和後驗機率8.5.4 置信集P-值第9章 區間估計...
