施泰納-萊默斯定理(Steiner-Lehmus theorem)是幾何學史中一個著名的定理,若一個三角形的兩條內角平分線相等,則此三角形是等腰三角形。這個命題是1840年萊默斯(C.L.Lehmus)在給斯圖姆(C.-F.Sturm)的一封信中提出的,他希望能用純幾何的方法證明,施泰納(J.Steiner)首先給出證明,施泰納的原證相當複雜,此後乃至近100年間還有這方面的文章,可見這個定理是何等引人入勝。
基本介紹
- 中文名:施泰納一萊默斯定理
- 外文名:Steiner-Lehmus theorem
- 所屬學科:數學(平面幾何)
- 提出者:萊默斯(C.L.Lehmus)
基本介紹,間接證法,直接證法,
基本介紹
施泰納-萊默斯定理(Staeiner-Lehmus theorem) 有兩條角平分線相等的三角形是等腰三角形。
這個問題是萊默斯(C.L.Lehmus)於1840年給瑞士著名數學家斯圖姆的一封信中提出的,請求給出一個純幾何的證明,斯圖姆向許多數學家提起過這件事。首先回答這個問題的是瑞士的幾何學家施泰納,後來這個定理就以施泰納一萊默斯定理聞名於世,由於施泰納的證明複雜,因而吸引了很多人去尋找更為簡單的證法,從而在1842至1864年間形成了證明施泰納-萊默斯定理的熱潮,乃至於在各種雜誌上出現了大量的證明論文,並在其後的一個世紀中,還經常有這方面的文章出現。
間接證法
下面給出的證法,是兩個英國工程師G.Gilbert和D. Macdonnell提出,在1963年《美國數學月刊》上發表的。
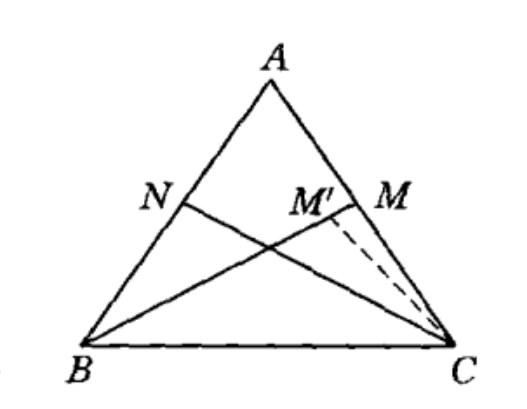
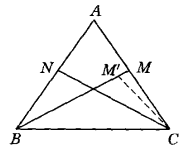 圖1
圖1設BM、CN是△ABC的兩條角平分線,且BM = CN,假設∠B≠∠C,不妨設∠B<∠C,則有


∴∠M'CN=∠M'BN,故B、C、M'、N四點共圓。
∴CN<M'B(同圓或等圓中兩圓周角都是銳角,則較小角所對的弦較短)。
於是有 CN<BM'<BM,這與題設CN=BM矛盾,故應有∠B=∠C,所以△ABC是等腰三角形。
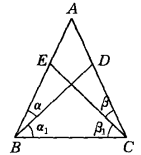 圖2
圖2考察上面的證法,可得一個更為廣泛的定理:“設D、E分別是OABC兩邊AC、AB上的點,記∠ABD=α,∠DBC=α1,∠ACE= β,∠ECB=β1,如果α:α1=β:β1=t,且BD =CE,則AB= AC。”顯然,當t= 1時,就是斯泰納萊默斯定理。
直接證法
上面採用的是間接證法(即反證法),同樣該定理也可採用直接證法來證,如圖3,把△BNC契約變換為△PBM,得MP = BC,∠PMB = β,∠PBM=∠BNC,PB= BN,於是
∠PMC=∠PMB+∠BMC
= β+(π-α-2β)
=π-α-β,
∠PBC=∠PBM+∠MBC
=(π-β-2α)+α
=π-α-β,
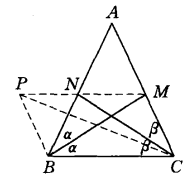 圖3
圖3而α+β=1/2(π-∠A)<π/2,故∠PMC=∠PBC為鈍角。
又由MP=BC,PC=CP,於是△PBC≌△CMP,從而CM=PB = BN,故△NBC≌△MCB,α= β,因此AB = AC。
若採用計算方法來證明,則思路直接,易於理解掌握,但有時計算比較繁雜,我們記△ABC的三邊BC、AC、AB之長各為a、b、c,由面積關係 ,得
,得




由已知BM= CN = t,得

如果α< β,則上式左端為正,但c > b,於是右端為負;若α>β,則左端為負右端為正,這都是不可能的,故只有a= β。
由上面的證明,順便可得到三角形內角平分線的計算公式:

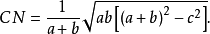
當然,如果利用上述三角形內角平分線的公式和BM = CN,並直接通過計算,那么就可得到b=c,這裡也許更體現了計算證法的特點。