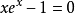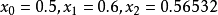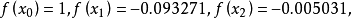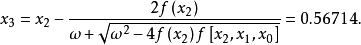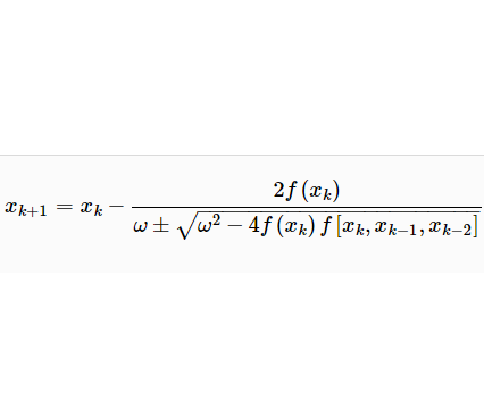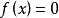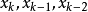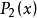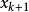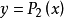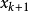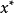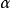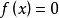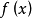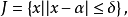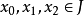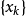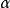拋物線法(parabolic approximate method)又稱二次插值法。用二次插值函式逼近未知函式而求解問題的方法。在結構最佳化方面系利用搜尋 區間內三個點的坐標和函式值構造二次函式來逐步逼近原一元函式,使搜尋區間逐步縮小並進而找到近似極小點的一維搜尋方法。也是一種常用的方法。設搜尋區間兩端點為a和b,其間有一點c, 相應的函式值分別為φd、φb和φc, 用它們構造一 個二次函式並解析地求得其極小點d,算得d點的函式值φd後, 可根據c、d的相對位置和φc與φd的大小確定留下具有搜尋區間應有性質的區間, 重複這個過程,使所留區間充分小,從而求得原一元函式的近似極小點。
基本介紹
- 中文名:拋物線法
- 外文名:parabolic method
- 別名:米勒法、二次插值法
- 所屬領域:計算數學(非線性方程數值解法)
基本介紹
幾何意義
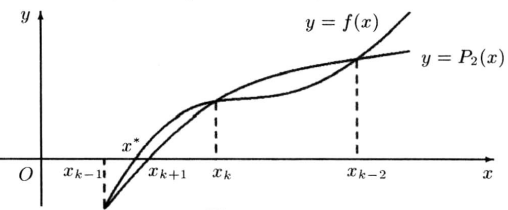 圖1
圖1計算公式推導
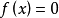
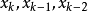
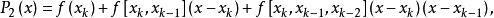

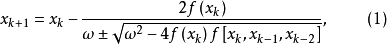
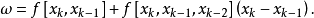
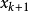
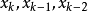
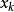
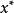

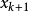
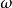
拋物線法的收斂定理
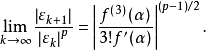
例題解析