拉格朗日反演

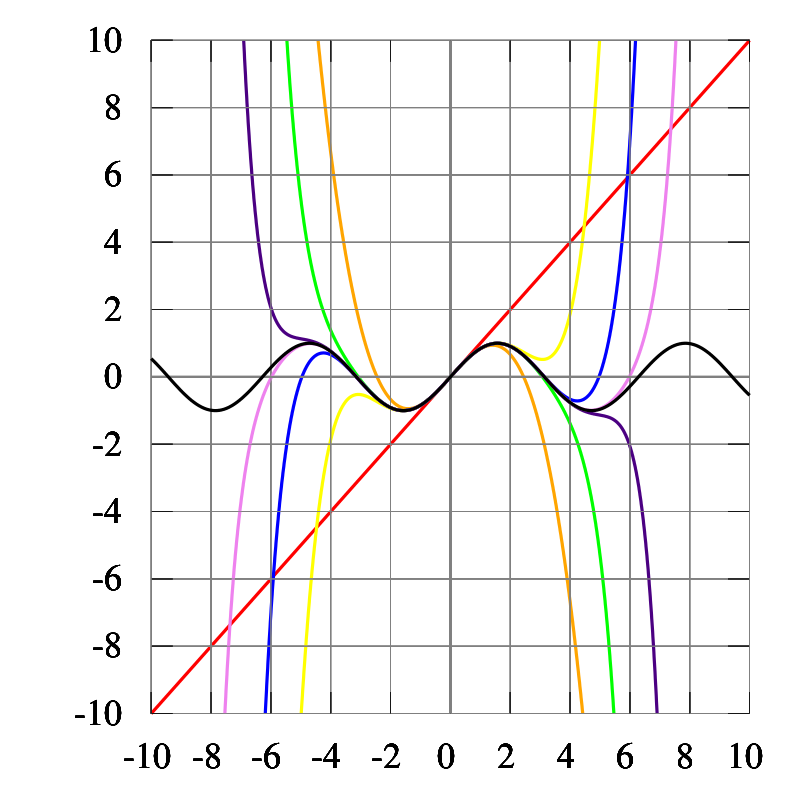
拉格朗日反演（Lagrange,1770）給出了解析函式的逆的冪級數表示，建立了函式方程和冪級數乘積之間的聯繫。

基本介紹

• 中文名：拉格朗日反演
• 外文名：Lagrange Inversion

概念

拉格朗日反演建立了函式方程和冪級數之間的聯繫，它解決的是這樣一個反演問題：

已知

尋求將y表為z的一個函式。為了保證反演法可用，還假定了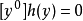 ，這樣反演在形式上是良定義的，並且還假定 ，以下為簡便起見，令 。

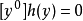
定理

令 為一個 中的冪級數， 。那么，方程 存在一個 中唯一的解：

其中，

而且，對k>0，(以下又稱Bürmann形式)

其中

如果H是任一函式，那么也有：

證明

這裡給個簡要的證明，可以由解析函式的性質判斷y(z)在0點是解析的，這樣 就可使用Cauchy定理：

這樣拉格朗日反演立得。

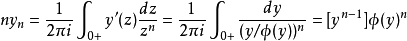
組合學解釋

拉格朗日反演在組合學中有對應的解釋，它和所謂的“共軛原則和環引理”相關。這裡考慮所謂的“Lukasiewicz paths”，它和波蘭表達式相關，但這裡從“格路問題”來說明，也就是從格路上的零點出發，每步的

位移用(f,g)表示，那么g=1，f取{-1,0,1,2,...}（下記做）但必須保證所有經過的點，除最後一步外，其餘點都在上半平面。n步的Lukasiewicz路徑的數目正好是卡特蘭數，。用L表示Lukasiewicz的組合類。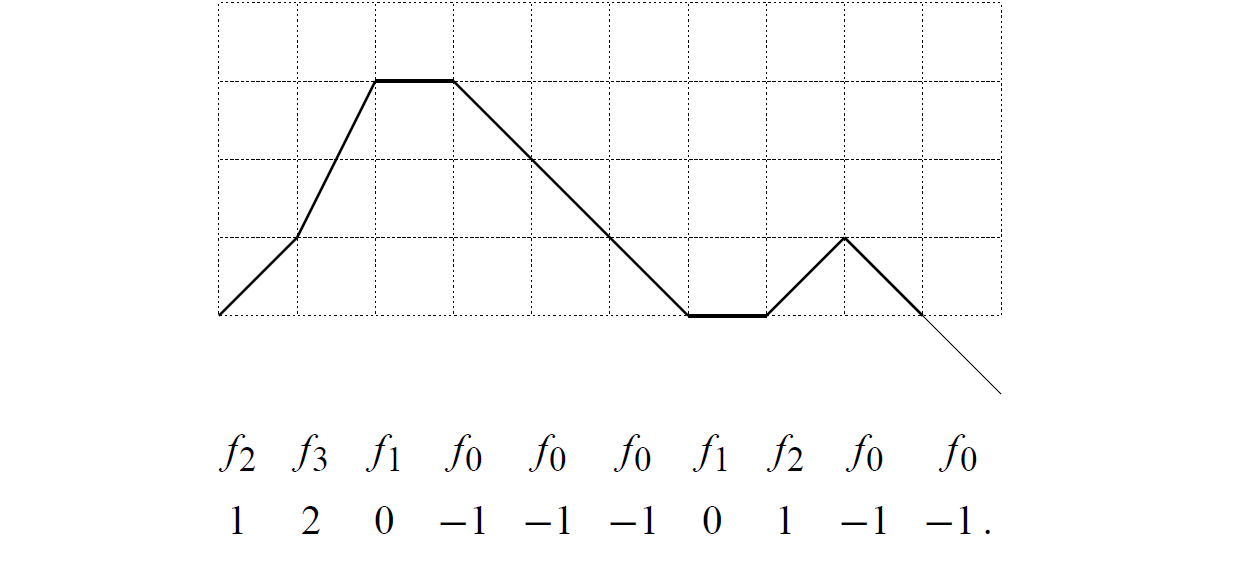

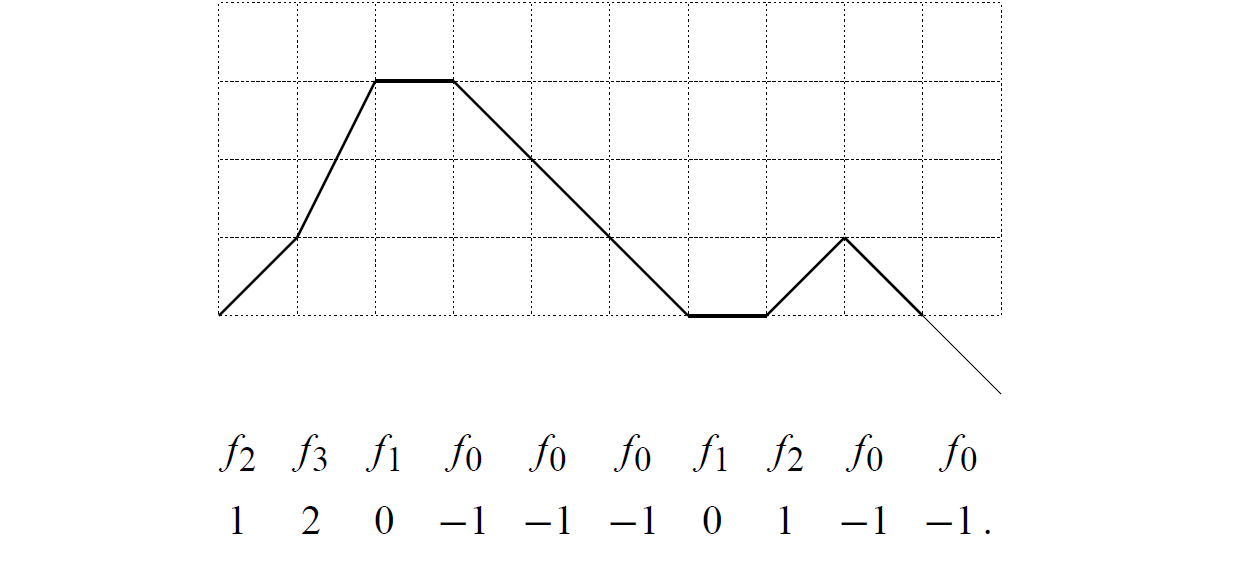
好的，我們定義“鬆弛”路徑滿足這樣的性質：開始於水平軸，最後終止在-1的高度上，與Lukasiewicz路徑的限制不同，這時允許中間經過任意的負點，令M表示對應的組合類。那么每一條“鬆弛”路徑可以唯一地通過其左方最低點“剪下和貼上”，從而變換成另一個標準的路徑：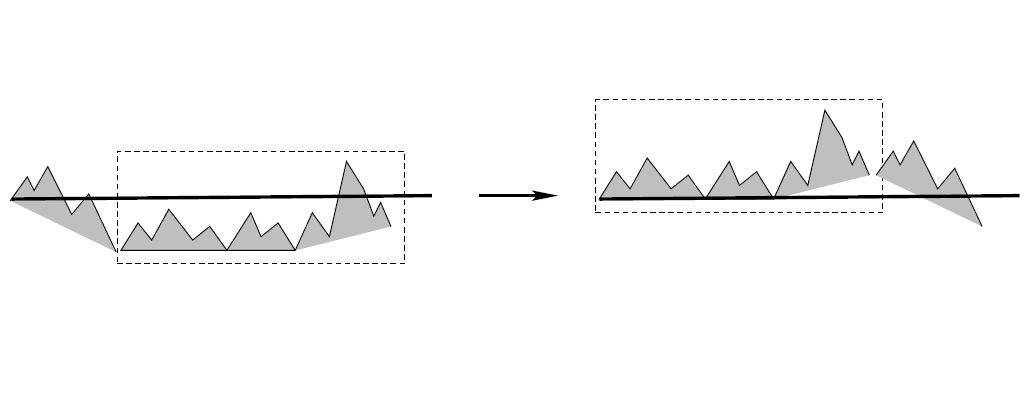

這樣每一條長度為的鬆弛路徑對應到一個標準路徑，當然這不是一一對應的，稍作思考，就可以發現這是1對的，也就是說L中的每個元素恰好有個原像。所以得到。這個對應保持了每個類型的f的數目，因此有步類型的Lukasiewicz路徑數為：

其中，。

這種由組合學的方式卡特蘭統計被稱作是共軛原則，或者是環引理。這在邏輯上是等價於拉格朗日反演定理。

套用

拉格朗日反演用處很多，在組合學中更是如此，這裡就舉組合學的例子來說明。

我們知道在圖論中，n個有標誌頂點的樹的數目等於，這是著名的Cayley定理。我們可以通過簡單的方法得到這個結果。為方便起見，我們認為這樣的樹中有一個根節點，令T表示這樣的有根樹所組成的類，那么由於是帶標誌的，同時子樹之間的順序不加區分，我們有符號化的結果：

翻譯到指數型生成函式就是：

這時我們看到這個有根樹T的指數型生成函式被一個函式方程隱式地定義了，如果對T(z)的冪級數展開式用待定係數法，我們或許可以看到：

注意到前幾個係數七號是，可以用拉格朗日反演定理直接得到的解析表示：

這時，由於所要求的是無根樹，因此在除以n即可。