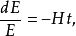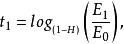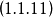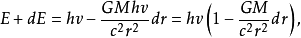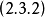微積開

微積開概念作為一種新的數學概念，其生命力在於：對適用問題的聯繫實際問題的高效率。

正如用ab與exp(lna+lnb)都可用於求解邊長為a與b的矩形面積。但ab具有聯繫實際問題“邊長為a與b的矩形面積”的高效率，筆算ab 的積卻效率差；而exp(lna+lnb)聯繫實際問題效率差，查對數表加筆算加法求exp(lna+lnb)相對於筆算ab的積的效率要高得多。因此在筆算時代，解決該實際問題總是先用ab聯繫實際問題“邊長為a與b的矩形面積”，

再用公式ab=exp(lna+lnb)將計算轉化為查對數表與加法筆算。

微積開概念就如同上述的ab那樣有聯繫實際問題的高效率，微積開的7個主要定理就如同上述的“公式ab=exp(lna+lnb)”那樣來解決計算的高效率：把微積開變換為微積分計算。

基本介紹

• 中文名：微積開
• 所屬學科：數學，物理
• 微積開發明：包學行
• 研究內容：動態切線，對數空間量綱，類星體
• 中心思想：未受思維束縛是如何創新解決問題
• 學科特點：理論嚴密、有廣泛套用前景

微積開概念的產生

微對數概念的萌芽

微積分是線性空間中思考問題的數學，它在處理非線性問題時聯繫問題變得較複雜。

現實中最多的非線性問題是與對數相關的問題。

例如：如果星光傳播中光子的能量有一非常小的損耗率，設光子單位時間損耗率為 H，在任一時刻t ，光子的能量為E，E₀為光子從光源發出（t = 0）時具有的能量，E₁為觀察到（t = t₁）時的光子具有的能量，設光速為c ，求星星的距離r與光子的能量為E₁關係。

解法1：

那么可建立微分方程

　

上式中的負號因定義 H 為損耗率而加，對上式(1.1)分離變數，得

　

兩邊積分，得

　

上式中C為任意常數，將初始條件代入上式，得

　

代入式(1.3)，得

　

移項，得

　

將邊界條件代入，得

　

將距離與時間的關係代入，得

　

由上式角解得

　

解法2：

如果，在對數空間考慮這個問題，光子經歷時間t₁就是以光子單位時間能量剩餘率(1-H)為底的光子能量剩餘率 的對數，即

　

也即

　

　

假定H為遠小於1一個很小的數，用解法2來解決該問題，就是微積開概念中的微對數概念的萌芽。

《微積開概念》作者（以下簡稱：作者）因文革中初二未學完就中斷學業，對上述問題只能產生解法2的思路，所以就產生了微對數概念的萌芽，但當時作者並未意識到這是微對數概念的萌芽。

定積開概念的產生

作者為了自已推導天體的引力紅移公式，他的思路是這樣的：按廣義相對論的質能關係， 具有能量 hv 的光子應具有質量 m = hv/c2, h為普郎克常數，v為光子頻率。那么一個質量為m 的光子脫離質量為M，尺度半徑為R的天體的表面至 ∞ 遠處必得作功消耗能量而引起光譜紅移，對於恆星發出的光子脫離其引力時，引力紅移是很小的，因此光子質量 m的變化也很小 ，先近似地設 m 為常量 ，設 G 為 萬有引力常數 ，R ≤ r ≤ ∞，r 為光子傳播路徑上光子與星體中心的距離， 那么光子脫離恆星，因作功的消耗，光子的能量變化值為（下式中的負號為引力方向與光子運動方向相反而加）

　

恆星的引力紅移可表示為

　

將(1.2.1)式代入，得

　

(1.2.3)式與廣義相對論的引力紅移公式最終引用計算式是一致的。這使作者意識到廣義相對論的引力紅移公式{即式（1.2.3）}僅是一條適用於弱引力紅移的公式，因為在他推導（1.2.3）式時近似設光子的質量 m 為常量。當一個光子脫離強引力場時，光子的質量變化很大，不能把光子質量作常量處理，所以（1.2.3）式不適用於強引力紅移。

因此作者就考慮要計算光子 m 在變化過程中對（1.2.1）式的積分。這本是一個用微分方程解的問題，但他當時還未自學到微分方程部分，用定積分又解不出了。他就用如下的方法解決了這個問題：

設 m = hv/c 為光子的瞬時質量， v 為光子在 r 處時的瞬時頻率，那么光子在距星體中心 r 處再遠離至 r + dr 處,在這 dr 路程中引力對光子作功

　

上式中的負號為引力的方向與光子的運動方向相反而加，在 r + dr 處剩餘的能量為

　

傳播距離 r 得增量dr後，能量變化倍率（比率）為

　

設光子在星體表面的頻率為 v₀ ，星體半徑為 R ，那么光子脫離星體表面至 ∞ 處它的能量將變為

　

上式中的足標表示變數在各時點上的值，用連乘積符號可把上式表示為

　

這就產生了一種和定積分有點類同的運算，定積分計算的是無窮多項的和，而（1.2.8）式計算的是無窮多個因子的積。作者當時把這種運算叫作乘積分，並把上述（1.2.8）式記作

　

後來作者對整個系統有進一步了解後，覺得應當把乘積分改稱為定積開更合理，詳見下文。

（文中圖片算式看不清請點擊圖片算式放大後看。）

微開方程概念的產生

後來作者分析了定積分與乘積分的關係，發現乘積分更確切應叫一個與定積分對應的名稱定積開，因為與微分對應有微開，與微商（導數）對應有微對數及微根二種，與不定積分對應有不定積開，與微分方程對應的微開方程有二種，一種為微對數方程，一種為微根方程。

我們都知道導數（微商）為常數的問題，如恆速運動的位移與時間的關係可用乘法計算，逆運算用除法；導數（微商）為非常數的問題，如變速運動位移與時間的關係可用定積分計算。

上述作者求解的類星體的紅移量與距離公式及引力紅移量公式問題，對應地為：

微對數為常數的問題，如類星體的紅移量與距離關係中，紅移量與時間的關係可用乘方計算，逆運算用對數；微對數為非常數的問題，如引力紅移公式可用定積開計算。

作者當時想類星體的紅移量與距離公式及引力紅移公式問題在微積分中是用微分方程解的問題，在微積開概念中都不用方程解，那么微積開概念中的微開方程將可解什麼問題呢？正在我百思不得其解的時候，一個巧遇使我得到了第一個線索。

因作者的父親數學較好，他退休後仍為《溫州醫學院學報》審稿，這天他正在審一篇有關統計的稿件，桌上正攤開一本參考書《衛生統計學》，翻在人口增展率 的定義這一頁上，作者發現人口增展率的定義就是微對數。

於是作者發現一個封閉域中的人口的演化與阻尼彈簧振子或 RLC充放電電路有對應關係。彈簧振子或 RLC 充放電電路的描述二階微分方程為

　

與

　

而一個封閉域中的人口的演化可由二階微根方程描述，即

　

（詳見下文介紹）。

微積開的基本概念

增率

增率是與增量對應的一種概念。

增率的定義 設函式 y = f(x) > 0 , 它在 x 點的某鄰域上有定義，在該鄰域內當 x 得到增量 ⊿x 時，則增率為

　

微對數

微對數是與微商（導數）對應的一種概念。

微對數的定義 設函式 y = f(x) > 0 , 它在點 x₀ 處若極限

　

存在，則此極限就稱作 f(x) 在點 x₀ 處的微對數，記作

　

如果每一個值 x₀∈D₁ 都唯一確定一個值 f(x₀)，則 f(x) 的微對數仍為定義在D₁域上的 x 的函式，記作

　

叫做 f(x) 的微對數函式，不過通常仍把 f^∨(x₀)了與 f^∨(x) 統稱為微對數。

定理1　設 f '(x) 存在，且 f(x) ≠ 0，則 f^∨(x)存在，並有

　

定理1證明　詳見參考文獻

微對數在人口統計學中的意義　詳見參考文獻

　　

微對數在原子物理中的意義

　我們知道高速粒子的運動質量為

　

對上式求微對數，得

　

上式中的

　

為德布羅意波的波速。

從(2.2.7)式可知，粒子運動質量對運動速度的微對數為該粒子相關的德布羅意波的波速與該粒子運動速度差的倒數。這種關係隱含著粒子的一種什麼特性呢？作者對原子物理知道得太少了，留給大家去思考吧。

微對數在動態幾何中的意義

在極坐標系中的軌跡Mm上（見圖1）的任一點 M的矢徑為OM，軌跡 Mm 的極坐標方程為

　

直角坐標系中的參數方程為

　

　

y軸從原點O指向上方，圖1中未畫出。這條軌跡在M點的的切線Mk與Ox軸的夾角為α，斜率為

　

現有一個動態直角坐標系vMu，M為該動態直角坐標系的原點，該原點M永遠位於軌跡Mm上，動態直角坐標系中的u軸永遠指向直角坐標系 xOy 的原點 O。 在動態直角坐標系 vMu 中軌跡 Mm 在 M 點（動態原點）的切線 Mk 與 Mv 軸的夾角為ψ，在三角形 OMk 中有

　

由上式解得

　

那么，在該動態直角坐標系 vMu 中軌跡 Mm 在 M 點的斜率為

　

因為

　

將(2.2.11)式代入上(2.2.15)式，得

　

將(2.2.16)式代入(2.2.12)式，得

　

由此可知極坐標中的軌跡方程(2.2.8)的微對數r^∨(θ) 即為動態坐標系 vMu中該軌跡的斜率（微商），即

　

微對數在其它學科中的意義簡述

此外推導一下即可明白：
微對數在銀行計息中的意義為利率;
　　微對數在放射性物質的衰變過程中的意義為衰變係數;
　　微對數在纜繩繞木樁牽力變化中的意義為力的衰變係數;
　　微對數在火箭動力學中的意義為燃料的消耗係數;
　　微對數在 RC 充放電電路中的意義為電路的 RC 時間常數，如果R 與C 為非常數的話：
　　微對數在 RC 充放電電路中的意義為電路的 RC 時間變數;
　　等等。

　　

微根

微根也是與微商（導數）對應的一種概念。

微根的定義

設函式y = f(x) >0, 它在點x₀處若極限

存在，則此極限就稱作f(x)在點x₀處的微根，記作

如果每一個值x₀∈D₂都唯一確定一個值f(x₀)，則f(x)的微根仍為定義在D₂域上的x的函式，記作

叫做f(x)的微根函式，不過通常仍把f(x₀)與f(x)統稱為微根。

定理2

設f'(x)存在，且f(x)≠ 0，則f(x)存在，並有

　

定理2證明　詳見參考文獻

微開

待續

不定積開

待續

定積開

底定積開

待續

指定積開

待續

冪定積開

待續

冪指定積開

待續

微開方程

微對數方程

待續

微根方程

待續

量綱危機及其解決

待續

繼續深入的問題

微積開有很多值得繼續深入的問題：

1) 因作者接觸的實際問題的面有限，微積開的套用面很需要廣大讀者聯繫自己接觸的實際問題，發現其新套用場合。

2) n 階的微對數方程是否存在求解方法？

4) 多重積開、曲線積開、曲面積開的套用面在哪？

5) 對應於微積分中的傅立葉變換的微積開“傅立葉變換”是否有特殊的套用意義？對應於微積分中的拉普拉斯變換的微積開“拉普拉斯變換”是否也有特殊的套用意義？以及其它的對應變換問題。

6)如果把微積開看成是對數空間中的一種“微積分”，那么任一單調函式構成的變換空間都可有該空間中的“微積分” , 把它稱為微積函，微積函的套用面又在哪呢？以及更一般的形式：任一單調函式構成的變換空間都可有該空間中的“斯底爾吉斯微積分”，把它稱為斯底爾吉斯微積函，斯底爾吉斯微積函的套用面又在哪呢？