定理及其證明
定理:一個
有向圖是
強連通的,若且唯若G中有一個迴路,它至少包含每個節點一次。
證明:
(1)充分性:如果G中有一個迴路,它至少包含每個節點一次,則G中任兩個節點都是互相可達的,故G是強連通圖。
(2)必要性:如果有向圖是強連通的,則任兩個節點都是相互可達。故必可做一迴路經過圖中所有各點。若不然則必有一迴路不包含某一結點v,並且v與迴路上的個節點就不是相互可達,與強連通條件矛盾。
強連通圖的邊問題
有n個頂點的強連通圖最多有n(n-1)條邊,最少有n條邊。
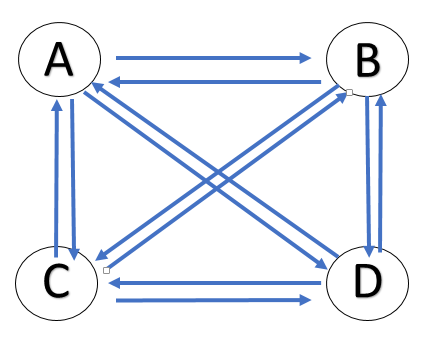 圖1
圖1(1)最多的情況:即n個頂點中兩兩相連,若不計方向,n個點兩兩相連有n(n-1)/2條邊,而由於強連通圖是有向圖,故每條邊有兩個方向,n(n-1)/2×2=n(n-1),故有n個頂點的強連通圖最多有n(n-1)條邊。
(2)最少的情況:即n個頂點圍成一個圈,且圈上各邊方向一致,即均為順時針或者逆時針,此時有n條邊。
下面舉例說明:如圖1所示,設ABCD四個點構成強連通圖,則:
(1)邊數最多有4×3=12條,如圖1所示。
(2)邊數最少有4條,如圖2所示。
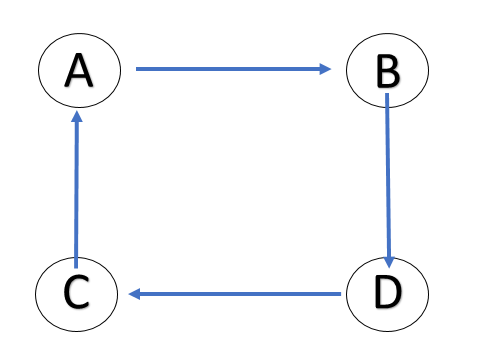 圖2
圖2強連通圖的判斷
問題:給一個有向圖,判斷給圖是否是強連通的。
如圖3所示,則是一個強連通圖。
對於無向圖則比較簡單,只需要從某一個頂點出發,使用
BFS或
DFS搜尋,如果可以遍歷到所有的頂點,則給定的圖是連通的。
但這種方法對有向圖並不適用,例如 : 1 -> 2 -> 3 -> 4,並不是強連通圖。
方法一
可以調用DFS搜尋 V 次,V是頂點的個數,就是對每個頂點都做一次DFS搜尋,判斷是否可達。這樣的複雜度為O(V*(V+E))。
方法二
可以參考求解連通分量的算法Tarjan算法,我們可以在O(V+E) 的時間內找到所有的連通分量,如果連通分量的個數為1,則說明該圖是強連通的。
#include <iostream>#include <list>#include <stack>using namespace std;class Graph{ int V; // 頂點個數 list<int> *adj; // 鄰接表存儲 // DFS遍歷,列印以v為起點的 強連通分量 void DFSUtil(int v, bool visited[]);public: Graph(int V) { this->V = V; adj = new list<int>[V];} ~Graph() { delete [] adj; } void addEdge(int v, int w); //判斷是是否是強連通圖 bool isSC(); // 得到當前圖的逆置 Graph getTranspose();};void Graph::DFSUtil(int v, bool visited[]){ visited[v] = true; list<int>::iterator i; for (i = adj[v].begin(); i != adj[v].end(); ++i) if (!visited[*i]) DFSUtil(*i, visited);}// 返回當前圖的轉置圖Graph Graph::getTranspose(){ Graph g(V); for (int v = 0; v < V; v++) { list<int>::iterator i; for(i = adj[v].begin(); i != adj[v].end(); ++i) { g.adj[*i].push_back(v); } } return g;}void Graph::addEdge(int v, int w){ adj[v].push_back(w);}bool Graph::isSC(){ bool visited[V]; for (int i = 0; i < V; i++) visited[i] = false; DFSUtil(0, visited); //如果有沒有被訪問的點就返回false for (int i = 0; i < V; i++) if (visited[i] == false) return false; // 創建當前圖的轉置圖 Graph gr = getTranspose(); for(int i = 0; i < V; i++) visited[i] = false; gr.DFSUtil(0, visited); // 查看是否是所有的點都被訪問到 for (int i = 0; i < V; i++) if (visited[i] == false) return false; return true;}// 測試int main(){ // 創建圖1 Graph g1(5); g1.addEdge(0, 1); g1.addEdge(1, 2); g1.addEdge(2, 3); g1.addEdge(3, 0); g1.addEdge(2, 4); g1.addEdge(4, 2); g1.isSC()? cout << "Yes\n" : cout << "No\n"; // 創建圖2 Graph g2(4); g2.addEdge(0, 1); g2.addEdge(1, 2); g2.addEdge(2, 3); g2.isSC()? cout << "Yes\n" : cout << "No\n"; return 0;} 圖1
圖1 圖2
圖2