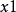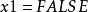基本定義和術語 命題邏輯公式,也稱為布爾表達式,由變數,運算符AND(連線,也用∧表示),OR(分離,∨), NOT (否定,¬)和括弧構成。如果通過為其變數分配適當的邏輯值(即TRUE,FALSE)可以使公式為TRUE,則稱該公式是可滿足的。給定公式,布爾可滿足性問題(SAT)是檢查它是否可滿足。這個決策問題在計算機科學的各個領域都至關重要,包括理論計算機科學,複雜性理論,算法,密碼學和人工智慧。
布爾可滿足性問題有幾種特殊情況,其中公式需要具有特定結構。文字是一個變數,稱為正文字,或變數的否定,稱為負文字。子句是文字(或單個文字)的分離。如果一個子句最多包含一個正文字,則該子句稱為Horn子句。如果公式是條款(或單個子句)的連線,則公式為合取範式(CNF)。例如,x1是正文字,¬x2是負文字,x1∨¬x2是子句,(x1∨¬x2)∧(¬x1∨x2∨x3)∧x1是聯合範式的公式;它的第一和第三個條款是Horn條款,但它的第二個條款不是。公式是可以滿足的,通過選擇x1 = FALSE,x2 = FALSE和x3任意,因為(FALSE∨¬FALSE)∧(¬FALSE∨FALSE∨x3)∧FALSE求值為(FALSE∨TRUE)∧(TRUE∨FALSE ∨x3)∧TRUE,依次為TRUE∧TRUE∧TRUE(即為TRUE)。相反,CNF公式a∧¬a由一個文字的兩個子句組成,是不可滿足的,因為對於a = TRUE或a = FALSE,它評估為TRUE∧¬TRUE或FALSE∧¬FALSE(即,分別為FALSE)。
對於SAT問題的某些版本,定義廣義联合範式公式的概念是有用的,即。作為任意多個廣義子句的連線,後者對於某些布爾運算符R和(普通)文字li具有R(l1,...,ln)形式。不同的允許布爾運算符集導致不同的問題版本。例如,R(¬x,a,b)是一個廣義子句,R(¬x,a,b)∧R(b,y,c)∧ R(c,d,¬z)是廣義的聯合正規形式。下面使用此公式,其中R是三元運算符,只有當其中一個參數為時才為TRUE。
使用布爾代數的定律,每個命題邏輯公式都可以轉換為等效的連線法線形式,然而,它可以指數地更長。例如,將公式(x1∧y1)∨(x2∧y2)∨...∨(xn∧yn)轉換為連線法線形式。
(x 1 ∨x 2 ∨…∨x n
(y 1 ∨x 2 ∨…∨x n
(x 1 ∨y 2 ∨…∨x n
(y 1 ∨y 2 ∨…∨x n
(x 1 ∨x 2 ∨…∨y n
(y 1 ∨x 2 ∨…∨y n
(x 1 ∨y 2 ∨…∨y n
(y 1 ∨y 2 ∨…∨y n
而前者是2個變數的n個連線的分離,後者由n個變數的2n個子句組成。
複雜性和受限制的版本 無限制的可滿足性 SAT是第一個已知的NP完全問題,1971年多倫多大學的Stephen Cook [2]和1973年國家科學院的Leonid Levin獨立證明了這一問題。在此之前,NP完全問題的概念甚至不存在。證明顯示複雜性類NP中的每個決策問題如何可以簡化為CNF公式的SAT問題,有時稱為CNFSAT。 Cook減少的一個有用特性是它保留了接受答案的數量。例如,確定給定圖形是否具有3色是NP中的另一個問題;如果一個圖表有17個有效的3色,那么Cook-Levin減少產生的SAT公式將有17個令人滿意的分配。
NP完全性僅指最壞情況實例的運行時間。實際套用中出現的許多實例可以更快地解決。請參閱下面的解算SAT的算法。
如果公式僅限於析取正規形式,即它們是文字連詞的脫節,那么SAT是微不足道的。若且唯若其連線中的至少一個是可滿足的時,這樣的公式確實是可滿足的,並且若且唯若它對於某個變數x不包含x和NOT x時,連線是可滿足的。這可以線上性時間內檢查。此外,如果它們被限制為完全分離正常形式,其中每個變數在每個連線中恰好出現一次,則可以在恆定時間內檢查它們(每個連線代表一個令人滿意的分配)。但是,將一般SAT問題轉換為析取範式可能需要指數時間和空間;例如,對於聯合正規形式,在上述指數爆炸示例中交換“∧”和“∨”。
3-可滿足性 與任意公式的可滿足性問題一樣,確定公式的可滿足性,其中每個條款限制為最多三個文字的連續正規形式也是NP完全的; 這個問題被稱為3-SAT,3CNFSAT或3-satisfiability。為了將無限制的SAT問題減少到3-SAT,將每個子句l1∨⋯∨ln轉換為n-2個子句的連線。
其中
是其他地方沒有出現的新變數。雖然這兩個公式在邏輯上不相同,但它們是完全可以滿足的。轉換所有子句得到的公式最多是其原始的3倍,即長度增長是多項式的。
3-SAT是卡普的21個NP完全問題之一,它被用作證明其他問題也是NP難的起點。這是通過從3-SAT到3-SAT的多項式時間減少來完成的。其他問題。使用此方法的問題的一個例子是clique問題:給定由c子句組成的CNF公式,相應的圖由每個文字的頂點和每兩個非矛盾文字之間的邊組成來自不同的條款,參見圖片。若且唯若公式可滿足時,該圖具有c-clique。
Schöning(1999)有一個簡單的隨機算法,該算法在時間(4/3)n中運行,其中n是3-SAT命題中的變數數,並且很有可能成功地正確決定3-SAT。
指數時間假設斷言在exp(o(n))時間內沒有算法可以解決3-SAT(或者實際上任何
的k-SAT)(即,基本上比n中的指數更快)。
3-SAT實例 Selman,Mitchell和Levesque(1996)給出了隨機生成的3-SAT公式難度的經驗數據,具體取決於它們的大小參數。難度是通過DPLL算法進行的數量遞歸調用來衡量的。
當考慮CNF中的公式時,3個可滿足性可以推廣到k-可滿足性(k-SAT,也就是k-CNF-SAT),每個子句包含多達k個文字。然而,因為對於任何
,這個問題既不比3-SAT更容易也不比SAT更難,後兩者是NP完全的,所以必須是k-SAT。
一些作者將k-SAT限制為具有k個文字的CNF公式。這也不會導致不同的複雜性類,因為每個子句l1∨⋯∨lj與j <k literals可以用固定的虛擬變數填充到l1∨⋯∨lj∨dj+1∨⋯∨dk。在填充所有子句之後,必須附加2k-1個附加條款以確保只有d1 =⋯= dk = FALSE才能產生令人滿意的賦值。由於k不依賴於公式長度,因此額外的條款導致長度不斷增加。出於同樣的原因,是否允許在子句中使用重複的文字(例如¬x∨¬y∨¬y)並不重要。
1-in-3-SAT 3-可滿足性問題的變體是三分之一3-SAT(也稱為1-in-3-SAT和恰好1-3-SAT)。給定一個帶有每個子句三個文字的連線法線形式,問題是確定是否存在對變數的真值賦值,以便每個子句只有一個TRUE文字(因此恰好是兩個FALSE文字)。相反,普通的3-SAT要求每個子句至少有一個TRUE文字。正式地,三分之一的3-SAT問題作為廣義联合正規形式給出,所有通用子句使用三元運算符R,如果其中一個參數是正確的則為TRUE。當三分之一的3-SAT公式的所有文字都是正數時,可滿足性問題被稱為三分之一正3-SAT。
三分之一的3-SAT及其正面案例在標準參考文獻中列為NP完全問題“LO4”,計算機和難以理解:由Michael R. Garey和David提出的NP完全性理論指南詹森。作為Schaefer二分法定理的一個特例,Thomas Jerome Schaefer證明了三分之一的3-SAT是NP完全的,該定理斷言任何以某種方式推廣布爾可滿足性的問題要么在P類中,要么是NP-完成。
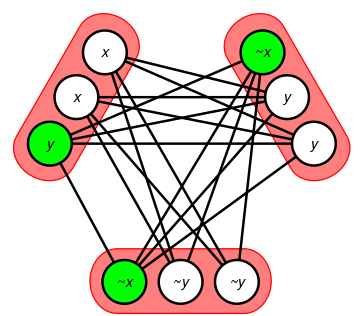
圖2 Schaefer提供了一種結構,允許從3-SAT到3-SAT三分之一的簡單多項式時間減少。設“(x或y或z)”是3CNF公式中的一個子句。添加六個新的布爾變數a,b,c,d,e和f,用於模擬此子句,而不是其他。那么公式R(x,a,d)∧R(y,b,d)∧R(a,b,e)∧R(c,d,f)∧R(z,c,FALSE)可滿足若且唯若x,y或z中的至少一個為真時,新變數的一些設定,見圖(左)。因此,任何具有m個子句和n個變數的3-SAT實例都可以被轉換為具有5m子句和n + 6m變數的等於三的3-SAT實例。另一個減少只涉及四個新變數和三個子句:R(¬x,a,b)∧R(b,y,c)∧R(c,d,¬z),見圖2。
SAT的擴展 自2003年以來獲得顯著普及的擴展是可滿足模數理論(SMT),其可以通過線性約束,數組,所有不同的約束,未解釋的函式,等來豐富CNF公式。這樣的擴展通常保持NP完全,但是可以使用有效的求解器來處理許多這樣的約束。
如果允許“for all”(∀)和“there there”(∃)量詞允許綁定布爾變數,則可滿足性問題變得更加困難。這種表達的一個例子是∀x∀y∃z(x∨y∨z)∧(¬x∨¬y∨¬z);它是有效的,因為對於x和y的所有值,可以找到適當的z值,即。如果x和y都為FALSE,則z = TRUE,否則z = FALSE。 SAT本身(默認)僅使用∃量詞。如果只允許∀量詞,則獲得所謂的重言式問題,即共同NP完全。如果允許兩個量詞,則該問題稱為量化布爾公式問題(QBF),可以顯示為PSPACE完全。人們普遍認為PSPACE完全問題比NP中的任何問題都嚴格,儘管尚未得到證實。使用高度並行的P系統,可以線上性時間內解決QBF-SAT問題。
普通的SAT詢問是否存在至少一個使公式成立的變數賦值。各種變體處理此類任務的數量:
MAJ-SAT詢問所有作業的大部分是否使公式為TRUE。眾所周知,PP是一種機率類。
#SAT,計算有多少變數賦值滿足公式的問題,是計數問題,而不是決策問題,並且是#P-complete。
UNIQUE-SAT是確定公式是否只有一個賦值的問題。對於美國來說,它是完整的,描述了由非確定性多項式時間圖靈機解決的問題的複雜性類,當只有一個非確定性接受路徑時它接受並拒絕否則。
當輸入限於具有至多一個令人滿意的賦值的公式時,UNAMBIGUOUS-SAT是給予可滿足性問題的名稱。允許UNAMBIGUOUS-SAT的求解算法在具有若干令人滿意的分配的公式上表現出任何行為,包括無限循環。雖然這個問題似乎更容易,但Valiant和Vazirani已經證明如果有一個實用的(即隨機多項式時間)算法來解決它,那么NP中的所有問題都可以很容易地解決。
MAX-SAT是最大可滿足性問題,是SAT的FNP推廣。它要求最大數量的條款,任何轉讓都可以滿足。它具有有效的近似算法,但是NP難以精確解決。更糟糕的是,它是APX完全的,意味著除非
,否則不存在針對該問題的多項式時間近似方案(PTAS)。
其他概括包括對一階和二階邏輯的可滿足性,約束滿足問題,0-1整數規劃。
自還原 SAT問題是可自我還原的,即如果SAT的實例是可解的,則正確回答的每個算法可用於找到令人滿意的分配。首先,詢問給定公式
的問題。如果答案是“否”,則公式不可滿足。否則,詢問部分實例化的公式
{
},即
,其中第一變數
被
替換,並相應地簡化。 如果答案為“是”,則
,否則
。隨後可以以相同的方式找到其他變數的值。總共需要
次算法運行,其中
是
中不同變數的數量。
這種自還原性在複雜性理論中用於幾個定理:

 3-SAT實例
3-SAT實例
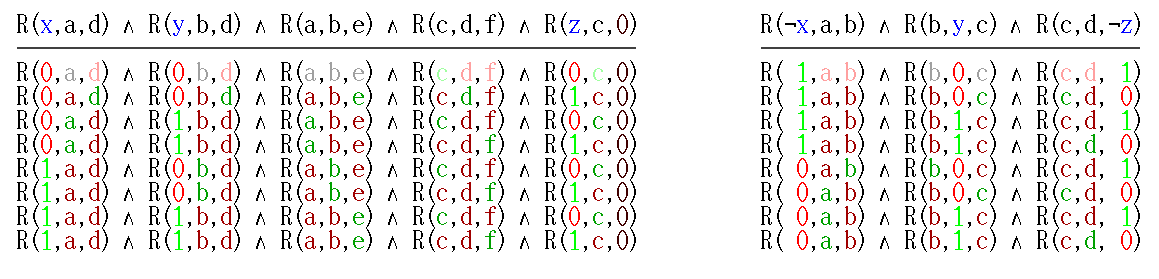 圖2
圖2