設M為元素取自交換體K中的n階方陣,將M對角化,就是確定一個對角矩陣D及一個可逆方陣P,使M=PDP-1。設f為典範對應於M的Kn的自同態,將M對角化,就是確定Kn的一個基,使在該基中對應f的矩陣是對角矩陣。
基本介紹
- 中文名:對角化
- 外文名:Diagonalize
- 所屬學科:數學
- 特點:只有主對角線上含有非零元素
- 相關概念:方陣,對角矩陣等
基本介紹
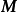




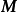
相關定理
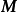

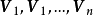

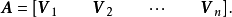

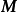

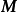




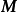

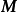
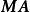


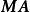


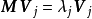
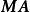


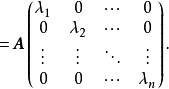




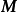

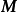



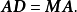




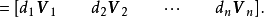

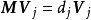




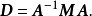
對角矩陣
定義
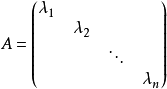



運算規律
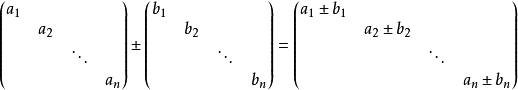


矩陣相似於對角矩陣的條件
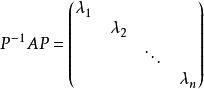


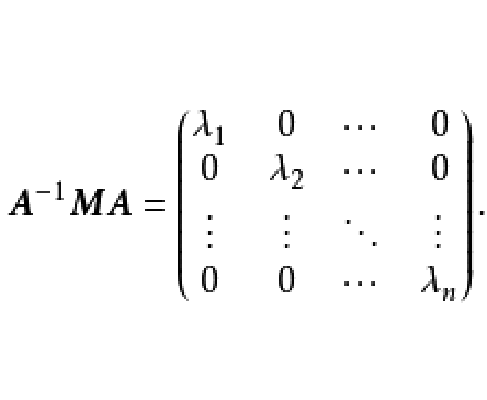
設M為元素取自交換體K中的n階方陣,將M對角化,就是確定一個對角矩陣D及一個可逆方陣P,使M=PDP-1。設f為典範對應於M的Kn的自同態,將M對角化,就是確定Kn的一個基,使在該基中對應f的矩陣是對角矩陣。
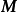




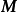
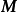

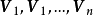

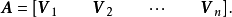

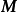

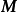




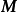

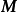
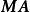


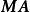


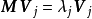
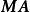


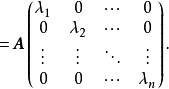




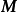

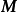



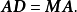




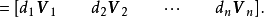

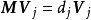




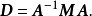
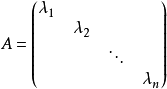



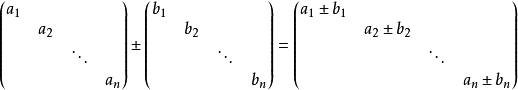


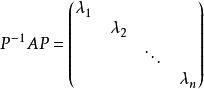


設M為元素取自交換體K中的n階方陣,將M對角化,就是確定一個對角矩陣D及一個可逆方陣P,使M=PDP-1。設f為典範對應於M的Kn的自同態,將M對角化,就是確定Kn...
可對角化矩陣是線性代數和矩陣論中重要的一類矩陣。如果一個方塊矩陣 A 相似於對角矩陣,也就是說,如果存在一個可逆矩陣 P 使得 P −1AP 是對角矩陣,則它就...
偽對角化是一種將矩陣化為對角優勢陣的方法.它是對給定的mXm復常數矩陣G=以,」,求一個實常數矩陣K = [k;; },使之左乘(右乘)G後所得的矩陣Q=KG(Q=...
精確對角化法(exact diagonaliation)是一個最直接求得基態的數值方法,但由於將哈密頓算符完整對角化非常花費時間與電腦記憶體,所以當需要的只是基態和少數激發態,通常...
對角矩陣(diagonal matrix)是一個主對角線之外的元素皆為0的矩陣,常寫為diag(a1,a2,...,an) 。對角矩陣可以認為是矩陣中最簡單的一種,值得一提的是:對角線...
在一個n階方陣(或是n階行列式)中,從左上角到右下角這一斜線上的n 個元素的位置,叫做n 階方陣(或行列式)的主對角線。...
只有對角線上有非0元素的矩陣稱為對角矩陣,或說若一個方陣除了主對角線上的元素外,其餘元素都等於零,則稱之為對角陣。...
《盲信源分離的聯合對角化方法研究》是張偉濤著寫的論文,由樓順天指導。...... 《盲信源分離的聯合對角化方法研究》是張偉濤著寫的論文,由樓順天指導。...
這很有用,因為對角化矩陣T的函式f(T)(譬如波萊爾函式f)的概念是清楚的。在採用更一般的矩陣的函式的時候譜定理的作用就更明顯了。例如,若f是解析的,則它的...
(7)若A與對角矩陣相似,則稱A為可對角化矩陣,若n階方陣A有n個線性無關的特徵向量,則稱A為單純矩陣。 (8)相似矩陣具有相同的可逆性,當它們可逆時,則它們的逆...
正規矩陣在數學中是指與自己的共軛轉置矩陣對易的復係數方塊矩陣。任意正規矩陣都可在經過一個酉變換後變為對角矩陣,反過來所有可在經過一個酉變換後變為對角矩陣...
任何n階復矩陣相似於復對稱矩陣。復對稱矩陣與實對稱矩陣的顯著區別之一是不一定能對角化,但是,對於復對稱矩陣仍然有類似於自伴矩陣譜定理那樣的分解。...
特徵分解(Eigendecomposition),又稱譜分解(Spectral decomposition)是將矩陣分解為由其特徵值和特徵向量表示的矩陣之積的方法。需要注意只有對可對角化矩陣才可以施以...
數學上,特別是線性代數和泛函分析中,譜定理是關於線性運算元或者矩陣的一些結果。泛泛來講,譜定理給出了運算元或者矩陣可以對角化的條件(也就是可以在某個基底中用對角...
若矩陣A可對角化,則其對角矩陣Λ的主對角線元素全部為A的特徵值,其餘元素全部為0。(一個矩陣的對角陣不唯一,其特徵值可以換序,但都存在由對應特徵向量順序組成...
《線性代數》包括行列式、矩陣、線性方程組、向量空間與線性變換、特徵值和特徵向量、矩陣的對角化,二次型及套用問題等內容。...
本書的內容包括線性方程組、n維向量空間、行列式、矩陣、矩陣的對角化問題、二次型及線性空間與線性變換共7章。最後的附錄“關於一元多項式的根的一些結論”給出了...
