多面體群,保持正多面體在空間占有位置不變的一切運動所成的群。一多面體在空間運動,其運動前後占有同一個空間位置,一切這樣的運動的集合。由歐拉定理推出:凸正多面體只有五種,即:正四面體、正八面體、正二十面體、正六面體(正方體)、正十二面體,其中正四面體、正八面體和正二十面體的各面都是正三角形,正六面體的各面是正方形,正十二面體的各面是正五邊形。
基本介紹
- 中文名:多面體群
- 外文名:polyhedral group
- 分類:群
- 對象:正多面體
- 特點:正多面體在空間占有位置不變
- 相似概念:二面體群
互為對偶的正多面體,正四面體群,正八面體群或正六面體群,多面體群簡介,二面體群,
互為對偶的正多面體
一個正多面體和以它的各面中心為頂的正多面體,叫做互為對偶的正多面體。
由歐拉定理推出:凸正多面體只有五種,即:正四面體、正八面體、正二十面體、正六面體(正方體)、正十二面體,其中正四面體、正八面體和正二十面體的各面都是正三角形,正六面體的各面是正方形,正十二面體的各面是正五邊形。
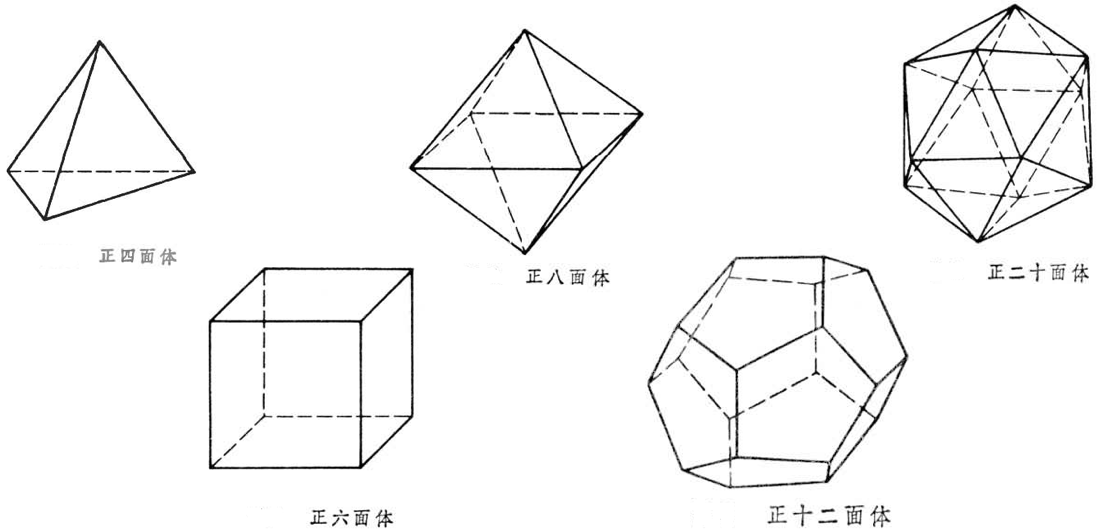
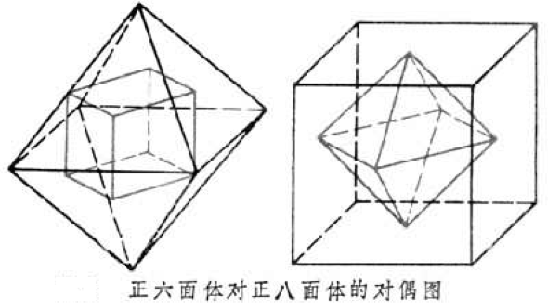
正六面體和正八面體是互為對偶的正多面體;正十二面體和正二十面體是互為對偶的正多面體;正四面體的對偶多面體是正四面體。
正四面體群
不動旋轉:
(A)(B)(C)(D)
以頂點與對面的中心連線為軸:
·A 為頂點(AO1):±120o (A)(BCD) and (A)(BDC)
·B為頂點:±120o (B) (ACD) and (B)(ADC)
·C為頂點:±120o (C) (ABD) and (C)(ADB)
·D為頂點:±120o (D) (ABC) and (D)(ACB)
共有8個三項循環。
以正四面體A-BCD的3對對邊之中點聯線為旋轉軸:作角度為π的3個旋轉,分別對應於置換(AB)(CD),(AC)(BD),(AD)(BC),
這樣的12個運動構成群,稱為正四面體群。
e, (BCD),(BDC),(ACD),(ADC),(ABD),(ADB),(ABC),(ACB) ,(AB)(CD),(AC)(BD),(AD)(BC),
它與4個文字A、B、C、D上的四次交錯群A4同構,因此,四次交錯群A4又稱為正四面體群。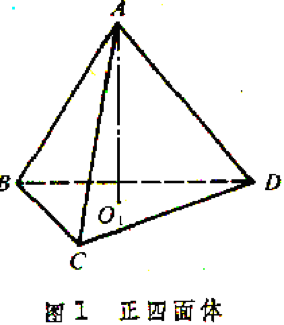

正八面體群或正六面體群
正八面體群或正六面體群由24個運動構成群,它與四次對稱群S4同構,所以正八面體群與正六面體群是一致的,都是4次對稱群S4。有時把四次對稱群稱為正八面體群或正六面體群。
多面體群簡介
保持正多面體在空間占有位置不變的一切運動所成的群。一多面體在空間運動,其運動前後占有同一個空間位置,一切這樣的運動的集合[151-01],對於以兩個這樣的運動相繼施行作為乘法構成群,稱為多面體群。由幾何學可知,正多面體只有5種,即正四面體、正六面體、正八面體、正十二面體、正二十面體。於是有正四面體群、正六(八)面體群、正十二(二十)面體群等三種群。
對於以兩個這樣的運動相繼施行作為乘法構成群,稱為多面體群。由幾何學可知,正多面體只有5種,即正四面體、正六面體、正八面體、正十二面體、正二十面體。於是有正四面體群、正六(八)面體群、正十二(二十)面體群等三種群。
在正四面體A-BCD中,以其正三角形BCD的中心O1與A點連結的直線AO1為軸,如圖1,將正四面體A-BCD按反時針方向繞AO1軸作角度為2π/3與4π/3的旋轉。顯然,這兩個旋轉運動分別對應於置換(BCD)與(BDC),且使正四面體在其運動前後占有同一空間位置。仿此,連結B點與正三角形ACD的中心O2的直線BO2為軸作角度為2π/3 與 4π/3的旋轉,這兩個旋轉運動分別對應於置換(ACD)與(ADC),並使正四面體在運動前後占有同一空間位置。同理,與置換(ABD)及(ADB),(ABC)及(ACB)所對應的旋轉,也使正四面體在運動前後占有同一空間位置。綜上所述共有8個三項循環:(BCD),(BDC),(ACD),(ADC),(ABD),(ADB),(ABC),(ACB)。它們分別對應的旋轉都是使正四面體占有同一空間位置的運動。再以正四面體A-BCD的3對對邊之中點聯線為旋轉軸, 作角度為π的3個旋轉,它們分別對應於置換(AB)(CD),(AC)(BD),(AD)(BC),並使正四面體占有同一空間位置。以I表示旋轉角為0的旋轉即不動旋轉,顯然,I是使正四面體占有同一空間位置的運動。總計共得12個旋轉運動。除此之外再沒有其他運動可保持正四面體占有空間位置不變。這樣的12個運動構成群,稱為正四面體群。它與4個文字A、B、C、D上的四次交錯群4同構,因此,四次交錯群4又稱為正四面體群。
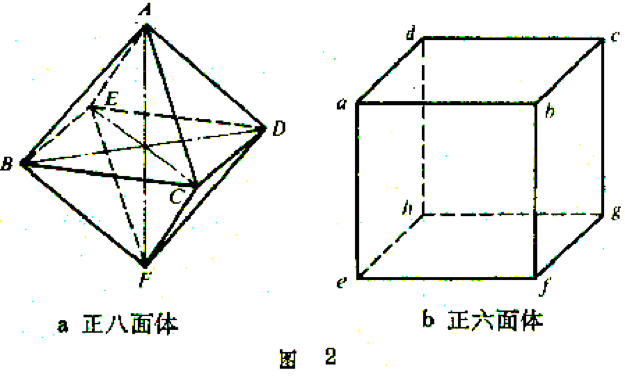
正八面體A-BCDE-F,其各個面都是正三角形,順次聯結各面的中心α,b,с,d,e,ƒ,g,h即得一個正六面體αbсd-eƒgh。對於正八面體A-BCDE-F分別以其 3條對角線AF,BD,CE為旋轉軸,作π/2,π,3π/2的旋轉,共有9個旋轉運動。它們都能使正八面體占有同一空間位置,同時使正六面體也占有同一空間位置。
以正八面體的4對對面的中心連線為旋轉軸,分別作π/3、2π/3的旋轉,共有8個這樣的運動。它們使正八面體,也使正六面體不變更所占的空間位置。再以正八面體的6對兩平行棱的中點聯線為軸作角度為π的旋轉,共有6個旋轉運動。它們使正八面體,並因之使正六面體不變更占有的空間位置。加上不動旋轉I,於是,使正八面體或正六面體不變更占有的空間位置的旋轉運動,總計有24個,且只有這24個。這樣的24個運動構成群,稱為正八面體群或正六面體群。它與四次對稱群4同構,所以正八面體群與正六面體群是一致的,都是 4次對稱群4。 有時把四次對稱群稱為正八面體群或正六面體群。
由於正十二面體的各面之中心的連線,可勾畫出正二十面體。因此,正十二面體群與正二十面體群是一致的。以正十二面體的 6對相對面的中心連線為軸作2π/5,4π/5,6π/5,8π/5的旋轉,這樣的旋轉共有24個。以10對相對頂點的連線為軸作 2π/3、4π/3的旋轉,這樣的旋轉共有20個。以15對相對對邊的中心連線為軸作π的旋轉, 這樣的旋轉共有15個。不動旋轉I一個。於是,使正十二面體或正二十面體不變更占有的空間位置的旋轉共有60個,且只有這60個。這樣的60個旋轉構成群,稱為正十二面體群或正二十面體群。它與5次交錯群5同構。
自然界中的晶體都呈規則的多面體外形,且同一種晶體物質總是結晶成相同的形狀,晶體還具有明顯的各向異性。這些自然現象都可以用上述群論方法來研究。晶體的結構是其原子按一定方式相互連結的空間點陣,稱為晶格。在這種點陣中可找到最基本的單位,稱為晶胞。整個點陣相當於晶胞按一定規則的排列。晶格具有上述五種正多面體或其他幾何體形狀。例如食鹽NaCl晶體的晶格就是正六面體形。
研究某種晶體的空間點陣時,有一些變換使空間點陣不變,這些空間變換不僅是前面所提及的旋轉運動,而且還包括平移、鏡面反射等運動。所有這些空間變換的集合成為一個群,稱為晶體的空間群或結晶群。它反映了晶體的內部結構和晶體的性質。結晶群中的所有平移的集合是一個正規子群,稱為平移子群。結晶群對其平移子群的商群,是一個類似於前面提到的多面體群的空間變換群,它刻畫了晶格以及晶體巨觀外形的對稱性質,稱為晶體點群。
晶體點群共有 32 個,其中包括正四面體群和正六(八)面體群。這是一個不太複雜而很有意義的結果。要得到與這32個晶體點群相聯繫的所有結晶群就複雜一些。一般的,從一個晶體點群出發,會發現多個結晶群以其為商群。儘管如此,結晶群的總個數也是不很多的,共有230個。找出這230個結晶群,並證明除此之外沒有其他的結晶群的工作,已在19世紀末由E.C.費德洛夫(1895)、A.舍福里斯(1896)和W.巴羅(1894)完成了。這一工作可以說是群論對其他自然科學的首次成功的重大套用,它也推動了群論本身的發展。
在正四面體A-BCD中,以其正三角形BCD的中心O1與A點連結的直線AO1為軸,如圖1,將正四面體A-BCD按反時針方向繞AO1軸作角度為2π/3與4π/3的旋轉。顯然,這兩個旋轉運動分別對應於置換(BCD)與(BDC),且使正四面體在其運動前後占有同一空間位置。仿此,連結B點與正三角形ACD的中心O2的直線BO2為軸作角度為2π/3 與 4π/3的旋轉,這兩個旋轉運動分別對應於置換(ACD)與(ADC),並使正四面體在運動前後占有同一空間位置。同理,與置換(ABD)及(ADB),(ABC)及(ACB)所對應的旋轉,也使正四面體在運動前後占有同一空間位置。綜上所述共有8個三項循環:(BCD),(BDC),(ACD),(ADC),(ABD),(ADB),(ABC),(ACB)。它們分別對應的旋轉都是使正四面體占有同一空間位置的運動。再以正四面體A-BCD的3對對邊之中點聯線為旋轉軸, 作角度為π的3個旋轉,它們分別對應於置換(AB)(CD),(AC)(BD),(AD)(BC),並使正四面體占有同一空間位置。以I表示旋轉角為0的旋轉即不動旋轉,顯然,I是使正四面體占有同一空間位置的運動。總計共得12個旋轉運動。除此之外再沒有其他運動可保持正四面體占有空間位置不變。這樣的12個運動構成群,稱為正四面體群。它與4個文字A、B、C、D上的四次交錯群4同構,因此,四次交錯群4又稱為正四面體群。
正八面體A-BCDE-F,其各個面都是正三角形,順次聯結各面的中心α,b,с,d,e,ƒ,g,h即得一個正六面體αbсd-eƒgh。對於正八面體A-BCDE-F分別以其 3條對角線AF,BD,CE為旋轉軸,作π/2,π,3π/2的旋轉,共有9個旋轉運動。它們都能使正八面體占有同一空間位置,同時使正六面體也占有同一空間位置。
以正八面體的4對對面的中心連線為旋轉軸,分別作π/3、2π/3的旋轉,共有8個這樣的運動。它們使正八面體,也使正六面體不變更所占的空間位置。再以正八面體的6對兩平行棱的中點聯線為軸作角度為π的旋轉,共有6個旋轉運動。它們使正八面體,並因之使正六面體不變更占有的空間位置。加上不動旋轉I,於是,使正八面體或正六面體不變更占有的空間位置的旋轉運動,總計有24個,且只有這24個。這樣的24個運動構成群,稱為正八面體群或正六面體群。它與四次對稱群4同構,所以正八面體群與正六面體群是一致的,都是 4次對稱群4。 有時把四次對稱群稱為正八面體群或正六面體群。
由於正十二面體的各面之中心的連線,可勾畫出正二十面體。因此,正十二面體群與正二十面體群是一致的。以正十二面體的 6對相對面的中心連線為軸作2π/5,4π/5,6π/5,8π/5的旋轉,這樣的旋轉共有24個。以10對相對頂點的連線為軸作 2π/3、4π/3的旋轉,這樣的旋轉共有20個。以15對相對對邊的中心連線為軸作π的旋轉, 這樣的旋轉共有15個。不動旋轉I一個。於是,使正十二面體或正二十面體不變更占有的空間位置的旋轉共有60個,且只有這60個。這樣的60個旋轉構成群,稱為正十二面體群或正二十面體群。它與5次交錯群5同構。
自然界中的晶體都呈規則的多面體外形,且同一種晶體物質總是結晶成相同的形狀,晶體還具有明顯的各向異性。這些自然現象都可以用上述群論方法來研究。晶體的結構是其原子按一定方式相互連結的空間點陣,稱為晶格。在這種點陣中可找到最基本的單位,稱為晶胞。整個點陣相當於晶胞按一定規則的排列。晶格具有上述五種正多面體或其他幾何體形狀。例如食鹽NaCl晶體的晶格就是正六面體形。
研究某種晶體的空間點陣時,有一些變換使空間點陣不變,這些空間變換不僅是前面所提及的旋轉運動,而且還包括平移、鏡面反射等運動。所有這些空間變換的集合成為一個群,稱為晶體的空間群或結晶群。它反映了晶體的內部結構和晶體的性質。結晶群中的所有平移的集合是一個正規子群,稱為平移子群。結晶群對其平移子群的商群,是一個類似於前面提到的多面體群的空間變換群,它刻畫了晶格以及晶體巨觀外形的對稱性質,稱為晶體點群。
晶體點群共有 32 個,其中包括正四面體群和正六(八)面體群。這是一個不太複雜而很有意義的結果。要得到與這32個晶體點群相聯繫的所有結晶群就複雜一些。一般的,從一個晶體點群出發,會發現多個結晶群以其為商群。儘管如此,結晶群的總個數也是不很多的,共有230個。找出這230個結晶群,並證明除此之外沒有其他的結晶群的工作,已在19世紀末由E.C.費德洛夫(1895)、A.舍福里斯(1896)和W.巴羅(1894)完成了。這一工作可以說是群論對其他自然科學的首次成功的重大套用,它也推動了群論本身的發展。
二面體群
二面體群是一種具體的群。保持平面上正n(n>2)邊形Rn不變的線性變換所成的群。它由保持Rn不變的n個旋轉和n個反射所組成。通常記為D2n.D2n是2n階的非交換群。從生成的角度來定義,二面體群是由兩個不同的特殊元所生成的群,即它有如下的定義關係:

