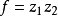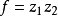基本介紹
- 中文名：多複變函數
- 外文名：function of several complex variables
- 學科：數學
- 性質：研究復變數全純函式的性質和結構
- 發展：把複分析推廣到任何多個自變數
- 相關理論：微分幾何學、代數幾何、李群等
簡介,歷史發展,多復變數的全純函式,解析開拓,零點的局部性質,全純域與Levi問題,
簡介
自從複變函數的理論被廣泛套用於數學的各個分支後，人們自然想把複分析推廣到任何多個自變數，以及任何多個因變數的復向量值函式上。多複變函數就是研究這類推廣的複變函數。
一開始，人們認為這種推廣只不過是形式上的照搬而已，但是很快人們就發現多複變函數與單複變函數有著許多差異。
首先，多複變函數什麼時候是全純函式？Hartoges 花了很大的力氣才證明：多複變函數全純若且唯若它對每個自變數都是全純的。 這個結論看似簡單，實則難矣。迄今為止，人們都沒有找到一個簡化的證明。
其次， 關於函式的延拓也存在著極大的差異。我們知道，複平面上任何單連通的開集上都存在一個單複變函數，它不能延拓到這個開集之外--滿足這種性質的開集叫做全純域。但是在多複變函數里卻發生了奇特的現象：有一些開鄰域，它們上面的任何全純函式都可以延拓到外面去。這種現象稱為Hartoges現象。 如果一個開鄰域不能發生Hartoges現象，我們就成這個鄰域為全純域。
歷史發展
多複變函數論的研究，早在單複變函數論的(G.F.)B.黎曼和K.(T.W.)外爾斯特拉斯時代就已經零散地開始了。但真正標誌著多複變函數論這一學科創立的，是19世紀末和20世紀初(J.-)H.龐加萊、P.庫辛、F.M.哈托格斯等人的工作。他們的研究揭示了多復變全純函式本質上的獨特性。在這當中，庫辛提出的關於全純函式整體性質的兩個以他命名的問題以及E.E.列維提出的擬凸域和全純域是否等價的問題，更有著深遠的影響，長時間成為多複變函數論發展的一個推動因素。20世紀30年代以前，雖然出現過K.萊因哈特關於解析自同構群、S.伯格曼關於核函式和度量等重要工作，但整個說來，多複變函數論處於相對沉寂的時期。從30年代開始，多復變的研究迎來了初步繁榮。這一時期中陸續出現了H.嘉當關於全純自同構的惟一性定理、有界域全純自同構群的李群性質以及全純域與全純凸的等價性的嘉當－蘇倫定理等突出成果。特別是從1936年開始，日本數學家□□對庫辛問題、列維問題、逼近問題等多復變的中心問題進行了長期、系統而富有成效的研究，終於在50年代對上述諸問題給出了解答。他的這一系列工作對以後年代的多復變的發展有著重大的影響。50年代以後，和近代數學的綜合化、抽象化的總潮流相一致，在多複變函數論中用拓撲方法和幾何方法研究全純函式的整體性質的趨勢變得越來越明顯。由J.勒雷引進拓撲學的層及其上同調的概念被迅速而成功地用於多復變。這一概念和H.嘉當早先關於全純函式理想論的研究以及□□的思想結合，導致了凝聚解析層理論的建立。與此同時，復空間和施泰因流形的概念也應運而生。H.嘉當和J.P.塞爾系統地套用凝聚層理論建立了施泰因流形的基本定理。此後不久，H.格勞爾特解決了複流形的列維問題，他和R.雷默特、施泰因等人還大大發展了復空間的理論。整個50年代無疑是多復變發展的黃金時代。
近代微分幾何與複分析的相互溶合也在不斷加快步伐。1913年，(C.H.)H.外爾的黎曼曲面理論導致了複流形概念的建立。□.(-J.)嘉當的外微分式與拓撲的結合產生了G.- W.德·拉姆的上同調理論。以此為基礎，W.V.D.霍奇將黎曼曲面上的調和函式理論推廣到高維的緊緻複流形，證明了緊複流形的基本定理──霍奇定理。40年代以後，與微分幾何中的博赫納技巧相結合，霍奇理論又由小平邦彥所發展和完善。60年代,博赫納－小平邦彥方法又進而推廣到非緊的帶邊界的複流形，發展成為近代多複分析的一個有力工具:□問題的L□估計。
多複變函數論中具有重要意義的第三方面進展是C.L.西格爾在1935～1950年間建立的多複變函數的自守函式論。50年代以後,由於A.賽爾伯格、R.朗蘭茲、И.□.蓋爾范德等人的工作，揭示了它與代數數論、李群的無窮維表示。
多復變數的全純函式
多復變全純函式研究的內容自然不是與單復變共同的性質，而是它的獨特性質。如解析開拓及零點的局部性狀等。
解析開拓
Hartogs發現，設K是
(n≥ 2)中一個域，K是K中的緊集，K-K連通，那么任何在K-K全純的函式都可以延拓到整個K，成為K上的全純函式。這種性質是單復變全純函式所決不具有的，與這種現象有關的研究構成了多複變函數論的基本內容之一(見全純域與Levi問題)。
零點的局部性質
單復變中全純函式的零點是孤立的,多複變函數的零點，即使從最簡單的例子
f=z1z2來看已經不再是孤立的，解析集的結構及多複變函數在其零點附近的性狀較之單復變的相應情況要複雜得多。
全純域與Levi問題
如果K是複平面C中的一個域，K~是另一個包含K而較大的域，那么總是存在K中全純而不能全純延拓到K~的函式(只要任取在K~中而不在K的一點a，考慮函式1/z-a即可)。這種現象在多複變函數中不再成立。從而導出全純域的概念，域K Cn稱為全純域，如果不存在更大的包含K的域K~，使任何K上的全純函式可以全純延拓到K~上。全純域的刻劃在多複變函數的歷史發展中長時期處於主導的地位。其中有一重要進展是:K是全純域的充要條件是K全純凸。從而更自然給出域的幾何刻劃。
定義：具有窮竭的多重次調和函式的域稱為擬凸域。根據Cartan Thullen定理，不難證明全純域是擬凸域。困難的、長期未解決的是其反面:擬凸域是否一定是全純域?這就是所謂Levi問題。五十年代中期Levi問題得以解決。Levi問題的解決引出了大量的，至今仍很活躍的推廣性研究。例如，對複流形而言的Levi問題就變成了什麼樣的複流形是Stein流形?
