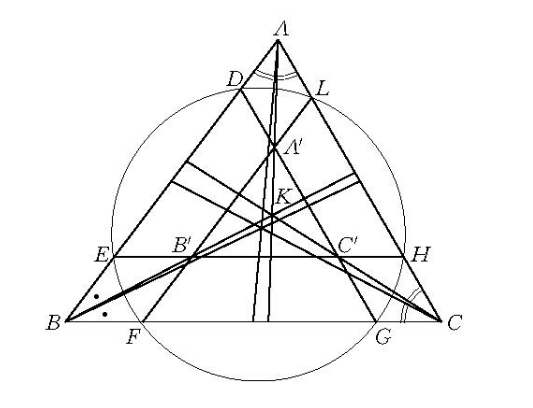
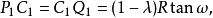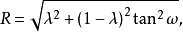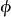塔克圓(Tucker circle)是關於幾個點共圓的問題，設K是△ABC的陪位重心，A′，B′，C′各是直線AK，BK，CK上的點，若A′B′∥AB，A′C′∥AC，則B′C′∥BC，且△A′B′C′與△ABC的非對應邊所在直線的六個交點D，E，F，G，H，L在同一個圓上，這個圓稱為△ABC的塔克圓。當A′，B′，C′三點依條件分別在直線AK，BK，CK上變動位置時，得到一系列的圓，稱為塔克圓系。
基本介紹
- 中文名：塔克圓
- 外文名：Tucker circle
- 所屬學科：數學
- 所屬問題：平面幾何（圓）
- 簡介：關於幾個點共圓的問題
- 特例：泰勒圓、萊莫恩圓、肯姆塔圓
塔克圓的概念,相關結論,塔克圓系,
塔克圓的概念
設K是△ABC的共軛重心，A'是AK上的點。
(1)若過A'作AB的平行線交KB於B'，過A'作AC的平行線交KC於C' ，則B'C' // BC。
(2)△A'B'C'與△ABC的非對應邊(所在直線)的六個交點共圓，如圖1。
該圓稱為△ABC的塔克(Tucker)圓。
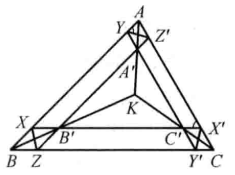圖1 塔克圓該結論是由英國數學家塔克提出的，當A’點在AK上變動時，就可以得到一群圓，稱它們為塔克圓系。
相關結論
1)由於KB'：KB=KA'：KA=KC'：KC，
所以B'C' // BC，同理A'B' // AB，A'C' // AC，K是△ABC和△A'B'C'的相似中心。
2)設A'B'分別交BC，AC於Z，Z'，B'C'分別交AB，AC於X，X'，A'C'分別交AB，BC於Y，Y'。
由於四邊形AYA'Z'是平行四邊形，AA'平分YZ’，又由於K是△ABC的共軛重心，因此YZ'必是BC的逆平行線，∠AYZ'=∠ACB=∠AX'X，故Y，Z'，X'，X四點共圓。
同理X，Z，Y'，Y四點共圓，Z'，Z，Y'，X'四點共圓，顯然上述三個圓實為同一圓，故X,X',Y,Y",Z,Z'六點共圓。
顯然，XZ,Y'X',YZ'是，上述圓中的三條等弦，因此塔克圓也可這樣確定。
在△ABC中，作三條相等的線段P1Q1，P2Q2，P3Q3與△ABC的邊分別逆平行，並且其中任意兩條，例如P2Q2與P3Q3不僅在BP2Q3C的同側，也在第三條線P1Q1的同側，則P2Q3P3Q2是等腰梯形。P3Q2，P1Q3，P2Q1分別與△ABC的相應邊平行，這些逆平行線的中點C1,C2,C3在相應的共軛中線上，並將這些共軛中線分成相等的比；設T將KO分成同樣的比，則TC1,TC2,TC3分別平行於半徑OA,OB,OC，並且TC1=TC2=TC3，如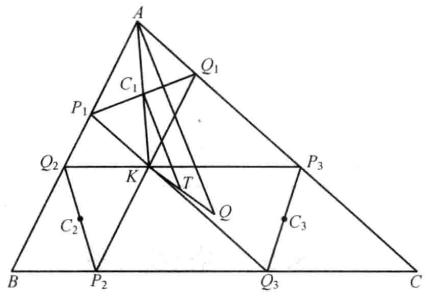圖2。
圖2因為逆平行線垂直於共軛中線，它們是一個以T為圓心的相等的弦，這個圓通過六個已知點P1，Q1，P2，Q2，P3，Q3，這個圓就是塔克圓。
塔克圓還有另一種作法，即從三角形一條邊上任意一點開始，作一個封閉的六邊形，它的邊交替地與三角形的邊平行或逆平行，至於開始先作逆平行線，還是先作平行線，則無關緊要，則逆平行的線段都相等，並且六邊形的頂點在一個塔克圓上，這樣的封閉六邊形稱為塔克六邊形，若在同一條邊上另取一點開始作塔克六邊形，這些六邊形都相似，且對應邊互相平行。
我們回到圖2，可以看出P2Q2，P3Q3與BC所成的角相等，都等於∠A，因此它們是等腰梯形的腰，我們又知道共軛中線平分逆平行線，所以C1,C2,C3在共軛中線上，但C2C3//P3Q2//BC，因此分BK，CK成比例。設
