基本介紹
基本介紹,舉例說明,
基本介紹
用直尺、圓規解幾何作圖問題,是一種傳統的規定,它是根據幾何公理確定的。關於限制工具的作圖問題,數學家們進行過許多研究,如尺規作圖問題,尺規作圖不能問題,單直尺或者單圓規作圖問題,即只用一個直尺或只用一個圓規進行作圖, 得出了一些重要的結果。
人們往往認為由於允許使用工具種類越多,則能解的作圖題範圍越廣,所允許使用的工具越少,則能解的作圖題的範圍便將縮小,其實並不如此。義大利數學家馬奢羅尼(L.Mascheroni, 1750-1800)在1799年發表了他的著作《圓規幾何學》,在這裡他提出了所謂單圓規作圖法。他證明了,如果我們認為“在平面上兩點得到確定時,則過此兩點的直線就被確定”,這時,所有用直尺和圓規能解的作圖問題,用單圓規便都能作出。因為初等幾何的作圖,實際上是確定點的問題,用直尺和圓規所能確定的點,不外三種情形:
(1)直線與圓的交點;
(2)直線與直線的交點;
(3)圓與圓的交點。
這三種情形得到完成,用作圖公法就都能得到完成。用單圓規可以完成(2),如果能用單圈規進行(1)、(2)兩種惰形的作圖,則上述“在平面上兩點得到確定時,則過此兩點的直線就被確定”中的結論就可得到證明。現在將(1)、(2)改述如下的形式:
(1)求作已知圓O (OA)與過二定點B、C的直線的交點。
(2)求作過二定點A、B的直線與過二定點C、D直線的交點。
馬奢羅尼證明了這兩個作圖是可能的。因此,凡用直尺圓規能作的作圖題,用單圓規都能作出。
法國的數學家彭賽列(Poncelet)在1822年,曾在他的著作《圖形的射影性質》里,論述了“在平面上已知一圓及其圓心時,則直尺和圓規能解的作圖問題,只用直尺就能得解”。當然,這裡所說的圓的確定,只要知其圓心及圓周上的一點就可以了。這一事實,在1833年斯太納(Steiner,德)的著作《一個定圓與直線可解的幾何作圖》里,有進一步的論述。因此,單直尺作圖問題,是彭賽列和斯太納共同完成的。為了證明單直尺作圖的可能,只要能解下列的兩個作圖就可以了.
(1)求已知圓心為A及該圓周上一點B的圓與定直線g的交點。
(2)已知四點A、B、C、D時,求圓A(AB)與C(CD)的交點。
而這兩個作圖,被證明是可能的,因此單直尺的作圖效能,也與直尺圓規相同。
舉例說明
尺規作圖歷史悠久,影響深遠,特別是古希臘三大幾何難題更是吸引了無數數學愛好者,尺規作圖看似簡單,其實奧妙無窮,具有挑戰性,能夠培養數學思維和數學能力。隨著人們數學水平的提高,從最開始的尺規作圖,又引發出了單規作圖、單尺作圖等更高難度的作圖。
下面介紹單尺作圖的幾個實例,並用面積法給出證明。
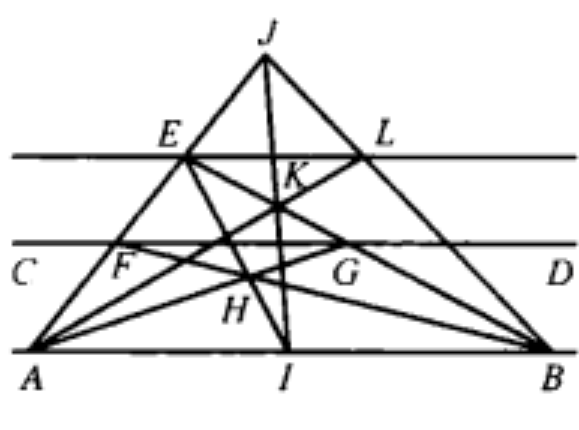
【例1】已知線段AB和平行於AB的直線CD,僅用直尺求作線段AB的中點。
【例1】已知線段AB和平行於AB的直線CD,僅用直尺求作線段AB的中點。
作法如圖1:
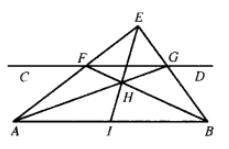 圖1
圖1(1)作出線段AB和直線CD;
(2)線上段AB和直線CD外任取點E,聯結AE、BE,分別交直線CD於點F、G;
(3)聯結AG、BF,交於點H;
(4)延長EH交AB於點I,點I即為所求。
證明

最後一步用到AB//CD,類似可證EH平分FG。這也是梯形中一個很有用的結論:延長梯形兩腰所得的交點和梯形兩對角線的交點的連線平分梯形的上底和下底。
1978年舉行全國中學生數學競賽時,數學大師華羅庚在北京主持命題小組的工作。著名數學家蘇步青寫信給華羅庚,建議出這個題目,但命題小組認為這個題目太難,改成“給出作好的圖形,只要證明",可見此題難度不小。
【例2】已知線段AB和平行於AB的直線CD,僅用直尺求作線段AB的n等分點。
作法 如圖2:
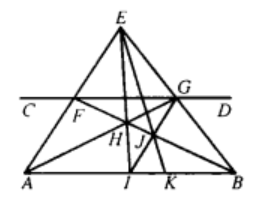 圖2
圖2(1)按例1的方法作出AB的中點I;
(2)聯結IG交BF於點J,延長EJ交AB於點K,則點K為AB的3等分點;
(3)類似操作即可得到線段AB的4等分點,5等分點...。
【例3】給定平行直線AB和CD,試過線外一點E,僅用直尺作平行於AB的直線。
作法 如圖3,先按例1的方法作出AB的中點I;在AE的延長線上任取點J ,聯結JI,交BE於點K;聯結JB,與AK的延長線交於點L;直線EL即為所求。
 圖3
圖3證明 因為