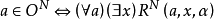可構造序數

可構造序數(constructive ordinal)是一種特殊的序數。α為可構造序數，是指存在一個記號系統S，使得S中有α的記號。可構造序數都是可數序數，可構造序數的全體構成序數的一個前節，並且可構造序數只有可數多個。從直觀上說，可構造序數是可以在自然數上能行表示的序數。事實上，對任何可構造序數，都存在遞歸相關的單一的記號系統S，使得S中有該序數的記號。此外，可構造序數也恰為遞歸序數。最早定義可構造序數並對之進行研究的是美國數學家、邏輯學家丘奇(A.Church)。

基本介紹

• 中文名：可構造序數
• 外文名：constructive ordinal
• 所屬學科：數學
• 所屬問題：數理邏輯(遞歸論)
• 提出者：丘奇(A.Church)

定義

給定如下條件：

(1) 任何一個自然數都不表示兩個不同的序數；

(2) 存在如下定義的三個部分遞歸函式 和 ：①對任何表示X的自然數，當X為零、孤立序數或極限序數時， 分別取值0 ，1，2；②當X為序數Y的直接後繼序數時，對表示的任何自然數而言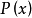， 表示Y；③當X為極限序數時，對表示X的任何自然數及每個自然數n而言， 表示 ，而 為一個遞增的序數序列，使得 。

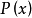
滿足上述條件(1)與(2)的自然數的集合稱為序數的記法系統(system ofnotation for ordinalnumbers)，把可用屬於一個記法系統的自然數來表示的序數稱為可構造序數。

S3系統

在序數的記號系統中，最有用和最方便的是 系統。設為以n為變元的原始遞歸函式，其定義為: ，用以下的遞歸定義引入系統 基本概念 和基本關係 ：

(1)

(2) 如果 ，則 並且 ；

(3 )如果自然數序列 具有性質：對每個n， 和 ，又如果 為這樣的 數，它把 作為 的函式而遞歸地定義，則 並且對每個n，有 ；

(4 )對 如果 並且 ，則 ；

(5) 只有由(1)-(4) 推得時，才有

對於 ，以下性質成立(為簡單起見，下面把( 簡寫成 )：

(1) 如果 ，則 ；

(2) 如果 ，則 ；

(3) 如果 ，則 ；

(4) 如果 ，則有自然數n，使得 ，這裡

(5)如果 則

(6) 如果 則對任何滿足 和 的數論函式 而言，均有k，使得

(7) 對每個

(8) 如果 並且 ，則 或 或 。

O中的每個元素a都可以依據下述方法而表示(reprsent)一個序數 對於 有 對於 和 ，有 設b為O的元素，則當 時，便有[a]<[b]；反之，對每個序數 均有一數a，使得 並且 。因此，集合 為關於≤的良序集並且它的序型為[b]。對O的每個元素a而言，均大於[a]的最小的數ξ與最小的不可構造的序數(在一些文獻中用ω₁表示) 是相同的。在S₃中，存在一個關於≤。良序的S₃的子系統，它對每個可構造序數α均具有一個唯一的記法(notation)。對這樣的子系統，可以取為(表示最外邊為全稱量詞的謂詞形的集合)集合K，使得K為O上的遞歸的集合。

相關定理

設 是關於自然數的謂詞。對於任意白然數 用 表示 成立。下面考察僅就集合 而言≤_R為線性有序的情況。如果D_R為關於≤_R的良序集，則用[R] 表示它的序型。於是：

(1) 對每個(可構造) 序數 存在一個一般遞歸(更嚴格地說，為原始遞歸)謂詞R，使得。

(2) 反之，如果R為超算術謂詞(R可以是一般遞歸的)，則。

(3) 集合O以及謂詞 都是 的，即對O而言，存在一個原始遞歸謂詞 使得 。

(4) 對每個序數 而言，集合{a|α>[a]}都是超算術集。

(5) O為 的完備集合，即對任意 集合E，存在一個原始遞歸函式φ，使得 。因此，O不是 (表示最外邊為存在量詞的謂詞形式的集合) 集合。

這裡的(3)與(4)是可構造序數理論中重要的有效定理，這兩個定理證實了kleene的解析譜系概念的正確性。給定一元(數論) 謂詞或給定一個自然數集合N，可以把可構造序數的概念關於N而相對化。令 表示關於N的最小的不可構造序數。記法系統S₃的基本概念和關係關於N而相對化後分別表示為和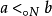，於是，上面的結果便可以關於N而相對化。例如，(3)的相對化的結果為:存在一個關於N一致的原始遞歸謂詞使得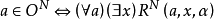。如果N為超算術的，則關於N而相對化並非會帶來擴充，即是成立的，但是當關於O 而進行相對化時，則可以獲得它的真正的擴充如果繼續進行這種推廣，則得到一個(超窮的) 序列另一方面，可以把可構造序數的概念不限於第二級數類而向更高的任意級數類進行推廣。但是，有關這方面的工作，並沒有象第二級數類那樣獲得很多的良好的結果。