在彈性力學中所發展的半逆解法就是針對所要求解的問題,先在待求應力分或位移分量中假設一部分未知函式的形式,然後將所假設的未知函式代入基本方程,並使全部的未知函式滿足所給定的邊界條件,求出另外一部分未知函式,得到問題的完整解答。
基本介紹
- 中文名:半逆解法
- 外文名:Semi-inverse method
- 例子:柱體扭轉和彎曲
簡介
半逆解法運用
扭轉
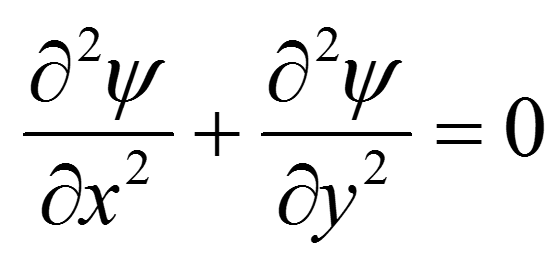
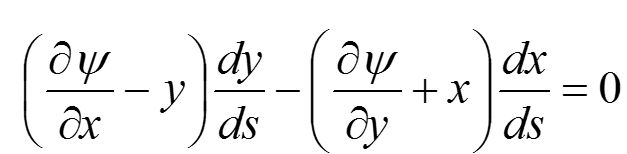
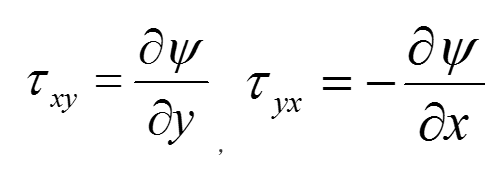
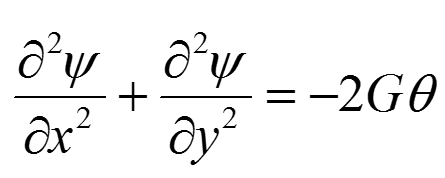
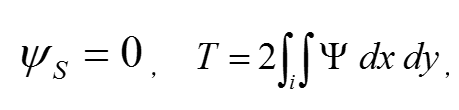
彎曲

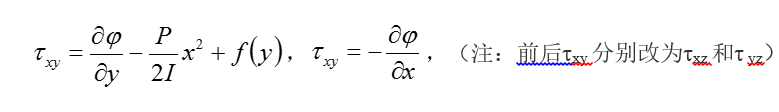

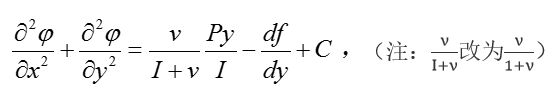




在彈性力學中所發展的半逆解法就是針對所要求解的問題,先在待求應力分或位移分量中假設一部分未知函式的形式,然後將所假設的未知函式代入基本方程,並使全部的未知函式滿足所給定的邊界條件,求出另外一部分未知函式,得到問題的完整解答。
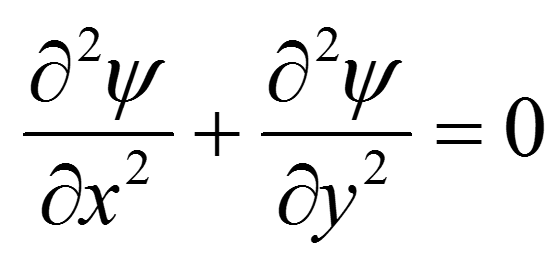
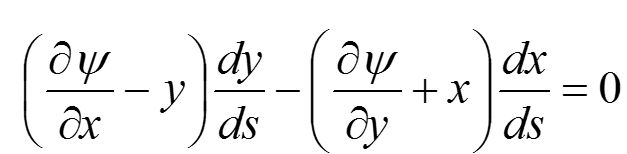
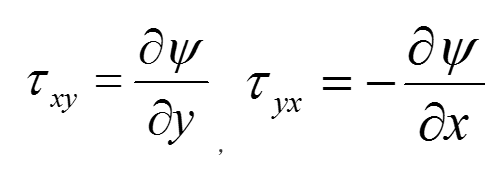
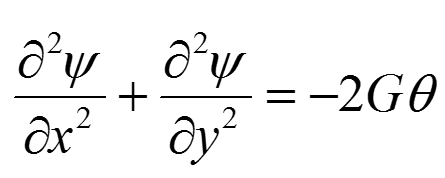
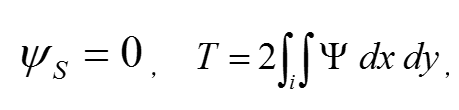

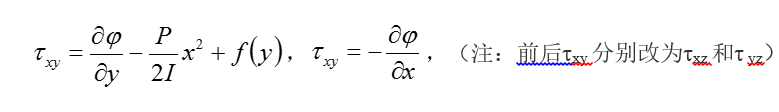

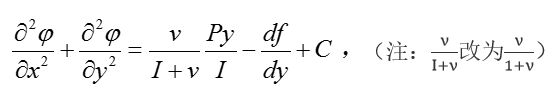




在彈性力學中所發展的半逆解法就是針對所要求解的問題,先在待求應力分或位移分量中假設一部分未知函式的形式,然後將所假設的未知函式代入基本方程,並使全部的未知...
聖維南的研究領域主要集中於固體力學和流體力學,特別是在材料力學和彈性力學方面作出很大貢獻,提出和發展了求解彈性力學的半逆解法。 由於聖維南取得了大量創造性的研究...
在非圓形截面柱體的扭轉問題中,截面不僅產生轉動,而且產生翹曲。下面介紹求解這類問題的半逆解法和薄膜比擬方法。柱體扭轉和彎曲半逆解法 ...
法國的A.J.C.B.de聖維南於1855年用半逆解法解出了柱體扭轉和彎曲問題,並提出了有名的聖維南原理。隨後,德國的F.E.諾伊曼建立了三維彈性理論,並建立了研究圓...
3.5.1 逆解法與半逆解法3.5.2 多項式應力函式的解答思考題3.6 矩形截面梁的純彎曲思考題3.7 承受端荷載的懸臂樑思考題3.8 承受均布荷載的簡支梁...
第一篇彈性力學,介紹了應力分析、應變分析、Hooke定律和空間問題的基本方程及柱體扭轉,重點講述彈性力學平面問題的解題方法,即用逆解法和半逆解法解平面問題,同時...
6.1 逆解法6.2 半逆解法第7章 等值截面柱體的扭轉與彎曲(Saint-Venant問題)7.1 位移法7.2 應力解法7.3 橢圓截面柱體的扭轉...
6.2平面彈性力學基本邊值問題的解法756.3應力函式776.4平面問題的逆解法、半逆解法與多項式解答796.5楔形體受重力和液體壓力的解876.6圓對稱的平面問題90...
1.8逆解法和半逆解法10習題11第2章平面問題122.1平衡方程122.2平面問題的幾何關係152.3平面問題的物理關係162.4用應力表示的協調方程182.5應力函式20...
5.1 應力函式、逆解法與半逆解法5.2 多項式解答——矩形梁純彎曲5.3 簡支梁受均布載荷5.4 楔形體受重力5.5 位移分量的求解習題6...
5.4 逆解法與半逆解法5.5 平面問題的極坐標解法5.6 關於塑性力學的解題方法第6章 屈服條件和塑性理論6.1 屈服條件6.2 兩種常用的屈服條件...
6.2 平面彈性力學基本邊值問題的解法 6.3 應力函式 6.4 平面問題的逆解法、半逆解法與多項式解答 6.5 楔形體受重力和液體壓力的解 6.6 圓對稱的平面問...
§2—12 應力函式逆解法與半逆解法 第三章 平面問題的直角坐標解答 §3—1 多項式解答 §3—2 矩形梁的純彎曲 §3—3 位移分量的求出 §3—4 簡支梁受均...
第三章 平面問題的直角坐標解答 3-1 逆解法與半逆解法 多項式解答 .3-2 矩形梁的純彎曲 3-3 位移分量的求出 3-4 簡支梁受均布荷載 3-5 楔形體受重力和...
3—1逆解法與半逆解法多項式解答3—2矩形梁的純彎曲3—3位移分量的求出3—4簡支梁受均布荷載3—5楔形體受重力和液體壓力習題第四章平面問題的極坐標解答...
4.3彈性力學問題的解法4.4彈性力學解的唯一性定理逆解法和半逆解法4.5局部影響原理(Saint-Venant原理)習題與答案第5章平面問題的直角坐標解答5.1平面問題的基本概念...
§1.2.7 逆解法和半逆解法§1.3 彈性力學平面問題的極坐標解答§1.3.1 極坐標下的基本方程§1.3.2 極坐標下的應力函式與相容方程...
在第一篇彈性力學中介紹了應力分析、應變分析、虎克定律和空間問題的基本方程及柱體扭轉,重點講述了彈性力學平面問題的解題方法,即用逆解法和半逆解法解平面問題 [...
第四節 逆解法與半逆解法——多項式解答 第五節 矩形梁的純彎曲 第六節 位移分量的求出 第七節 簡支梁受均布荷載 第八節 楔形體受重力和液體壓力 習題三 第...
逆解法與半逆解法 第三章 平面問題的直角坐標解答 §3—1 多項式解答 §3—2 位移分量的求出 §3—3 簡支梁受均布荷載 §3—4 楔形體受重力和液體壓力 §...
(基本概念、基本方程和基本解法)的闡述,突出解決彈性力學問題的思路、方法和步驟...3—1逆解法與半逆解法多項式解答 3—2矩形梁的純彎曲 3—3位移分量的求出...
彈性柱體扭轉問題的解決,一方面基於聖韋南原理,即在端頭放鬆邊條件;另一方面基於先假設問題的一部分未知量為已知,然後求未知的部分,即所謂半逆解法.設柱截面為xy...
學習指導§3-1 逆解法與半逆解法多項式解答§3-2 矩形梁的純彎曲§3-3 位移分量的求出§3-4 簡支梁受均布荷載§3-5 楔形體受重力和液體壓力例題...
4.4逆解法和半逆解法4.5邊界上φ及其導數的力學意義4.6平面問題的極坐標解法4.7關於塑性力學的解題方法4.8板條的彎曲問題習題第5章厚壁圓筒的分析...
第6章 平面問題的解法6.1 平面應力問題和平面應變問題6.2 平面彈性力學基本邊值問題的解法6.3 應力函式6.4 平面問題的逆解法、半逆解法與多項式解答...
3.5 位移解法與應力解法3.6 應力函式、逆解法及半逆解法習題3第4章 平面問題直角坐標解答4.1 代數多項式解答4.2 矩形梁的純彎曲問題4.3 簡支梁受均布荷載...
4?4逆解法和半逆解法1444?5邊界上φ及其導數的力學意義1504?6平面問題的極坐標解法1594?7關於塑性力學的解題方法1684?8板條的彎曲問題172習題177...
第一節 逆解法和半逆解法第二節 平面問題的多項式解答第三節 矩形截面梁的純彎曲第四節 簡支梁受均布荷載第五節 受自重和靜水壓力作用的楔形體小結...
17 2 3逆解法與半逆解法25717 3受均布載荷的簡支梁25817 4平面問題的極坐標解答26117 4 1極坐標系中的應力函式與協調方程26117 4 2軸對稱問題的應力和位移...
