半角模型

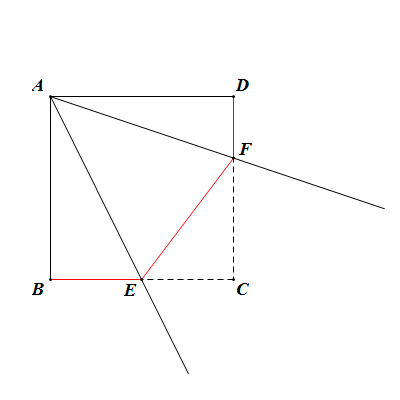
半角模型是指：從正方形的一個頂點引出夾角為45°的兩條射線，並連結它們與該頂點的兩對邊的交點構成的基本平面幾何模型。

由於兩射線的夾角是正方形一個內角的一半，故名半角模型，又稱“角含半角模型”。

其中，將45°角的兩邊及其對邊圍成的三角形稱為“半角三角形”（即圖中的△AEF）

半角模型的結論：

半角模型中射線與端點對邊交點的連線長等於端點兩相鄰點到各自最近交點的距離和。即：如圖中，EF=BE+DF。

基本介紹

• 中文名：半角模型
• 外文名：Half-angle Model
• 領域：數學-幾何

定義

從正方形的一個頂點引出夾角為45°的兩條射線，並連結它們與該頂點的兩對邊的交點構成的基本平面幾何模型稱為 半角模型 。

主要結論

結論一

半角模型中射線與端點對邊交點的連線長等於端點兩相鄰點到各自最近交點的距離和。

即如圖中，四邊形ABCD是正方形，點E,F分別在BC和CD邊上，滿足∠EAF=45°，連結EF，則有：EF=BE+DF。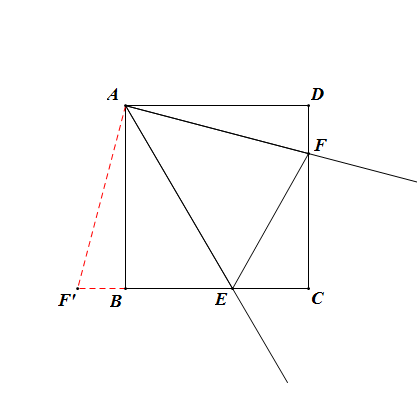

結論一的幾何證明

證明：

【證法一】（旋轉法）

∵四邊形ABCD是正方形，

∴AB=AD，∠D=∠ABE=90°；

將△ADF繞點A旋轉至△ABF'的位置（F的對應點為F'），則

△ADF≌△ABF'，∴∠BAF'=∠DAF，BF'=DF，AF=AF'；

∴∠EAF'=∠BAE+∠DAF=45°=∠EAF，

易證△AEF≌△AEF'(SAS)，∴EF=EF'=BF'+BE=DF+BE，

即EF=BE+DF。

（註：若將△ABE繞點A旋轉至△ADE'的位置亦可，證法類同）

【證法二】（截長補短法）

延長CB至點F'，使BF'=DF，連結AF'。

易證△ADF≌△ABF'(SAS)，∴AF=AF'，∠BAF'=∠DAF，

∴∠EAF'=∠BAE+∠BAF'=∠BAE+∠DAF=45°=∠EAF，

則△AEF'≌△AEF(SAS)，∴EF=EF'=BF'+BE=BE+DF，

即EF=BE+DF。

（註：若延長CD至點E'，使DE'=BE亦可，證法類同）

【證法三】（解析法）

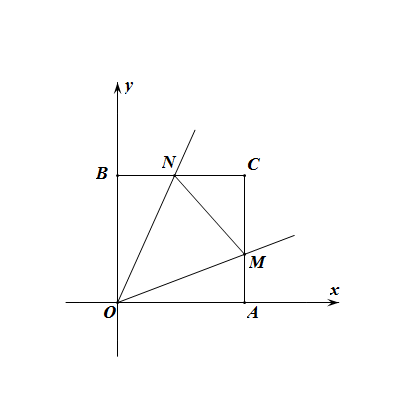
建立如圖的平面直角坐標系，則需要證：MN=AM+BN

設正方形OACB的邊長為a，直線OM的解析式為，∵∠MON=45°，

∴由兩角和公式，直線ON的斜率，則直線ON的解析式為。

綜上可得，點M、N的坐標分別為、，

∴，,

故原命題得證。

結論二

兩射線的公共端點是射線截端點兩對邊所得直角三角形的一個旁心，即射線平分截得的直角三角形兩銳角的外角。

證明：

由“結論一”的證明過程可得：

∠AEF=∠AEB，∠AFE=∠AF'E=∠AFD，根據旁心的定義即可證得點A為直角三角形CEF的旁心。

結論三

兩射線的端點到射線與端點兩對邊交點的連線的距離等於正方形的邊長。

即如圖中，作AH⊥EF於點H，則AH=AB。

證明：

【證法一】此性質可由結論二（旁心的性質）證得。

【證法二】由角平分線定理，可得AB=AH=AD

結論四

過兩射線的端點且垂直於射線與端點兩對邊交點連線的直線分“半角三角形”得的兩個三角形與半角三角形外的兩個小三角形分別全等。即圖中△AFD≌△AFH，△AEB≌△AEH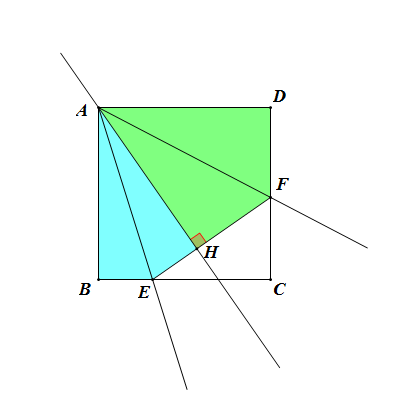

結論四

證明：

此結論容易由結論三並結合“HL”全等判定進行證明，故不再贅述。

當然由此也可以得到：

S△ABE+S△ADF=S△AEF

結論五

射線截端點兩對邊所得直角三角形的兩直角邊相等時，其斜邊長取到最小值，其面積取到最大值。

證明：由勾股定理，，當CE=CF時取等號，此時EF達到最小值，

直角三角形CEF的面積達到最大值。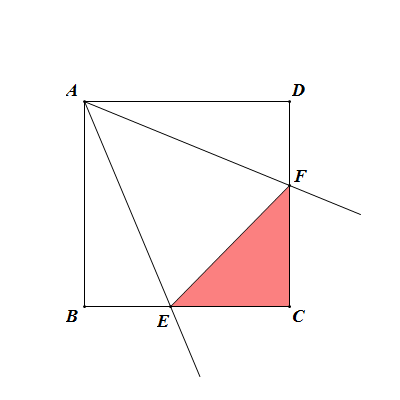

結論五

其它結論

當連結正方形的另一條對角線時，會得到更多結論。

證明過程僅選取主要方法，其他證法合理即可。

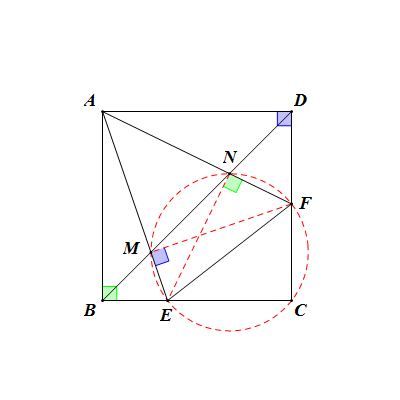
結論六

兩射線截另一條對角線所成的三條線段可以圍成一個直角三角形，且中間一條為斜邊。

即：如圖，AE、AF截BD於點M、N，則有： 。

證明：將△ADN繞點A旋轉至△ABN'的位置（點N對應點N'），連結MN'，

∴△ADN≌△ABN'，∴BN'=DN，∠BAN'=∠DAN，∠ABN'=∠ADN，

∴∠MBN'=90°，∠N'AM=∠NAM，易證△AMN'≌△AMN，∴MN'=MN

從而 ，即 。

結論七

共有五個三角形與△AMN相似：

第一組：如圖，△BME、△DNF與△AMN相似。

證明：由一組對頂角和一組相等的角（45°）即可證明。

第二組：如圖，△ABN、△ADM和△AMN相似。

證明：由一組公共角和一組相等角（45°）即可證明

第三組：如圖，△AEF與△AMN相似。

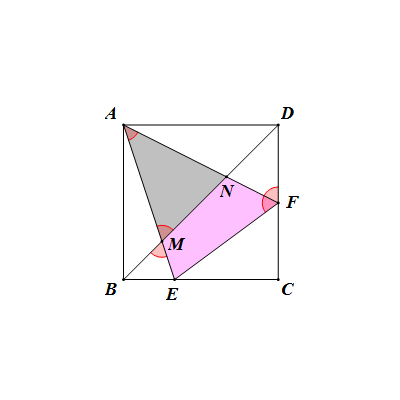相似三角形——第三組

證明：由一組公共角和∠AMN=∠AFE（或∠ANM=∠AEF）即可得到結論。其中∠AMN=∠AFE（或∠ANM=∠AEF）的證明如下：

由半角模型的結論二可得∠AFE=∠AFD；由第一組相似可得∠DFN=∠BME=∠AMN，從而∠AMN=∠AFE。（∠ANM=∠AEF的證明類同，故不再贅述）

結論八

圖形中也存在多組四點共圓。

第一組：A、B、E、N四點共圓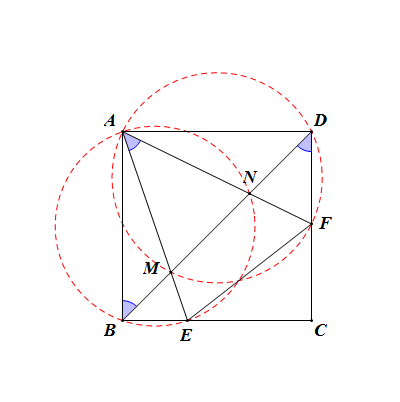

證明：∵∠EAN=∠EBN=45°，

由輔角定理可得A、B、E、N四點共圓。

第二組：A、D、F、M四點共圓

證明：∵∠MAF=∠MDF=45°，

由輔角定理可得A、B、E、N四點共圓。

第三組：C、E、F、N、M五點共圓

證明：∵∠BME=∠AMN=∠DFN=∠NFE，

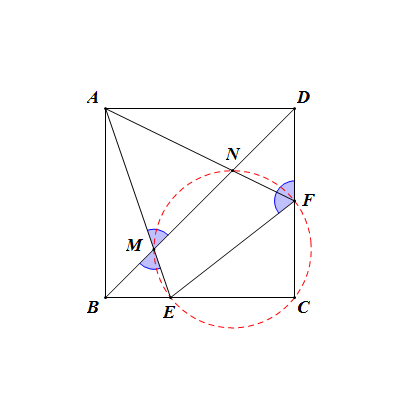
（已在結論七的第三組中詳細證明）

∴E、F、N、M四點共圓；

連結EN、FM，

由第一、第二組四點共圓可得∠ENF=∠EBA=90°，

∴∠ENF+∠C=180°，

∴C、E、N、F四點共圓，

從而C、E、F、N、M五點共圓。

逆定理

半角模型命題中的條件和結論可以分為以下幾條。其中以條件①為基礎，只要滿足其它任一條件，其它條件即可成為結論。

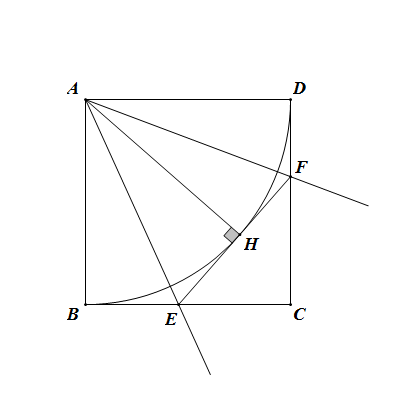
逆定理

①四邊形ABCD是正方形；

②∠EAF=45°；

③EF=BE+DF；

④點A是△CEF的旁心（EA、FA分別平分∠BEF、∠DFE）；

⑤AH=AB；

（其他結論均可推出，不再贅述）

下面逐一進行證明：（“→”前是條件，“→”後是結論。當①②同時成立時，其他結論作為半角模型的性質，不再證明）

①②→③④⑤

半角模型原命題，不再證明。

①③→②④⑤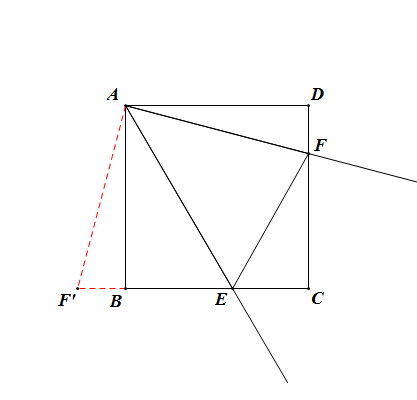

逆定理的證明（一）

證明：如圖，將△ADF旋轉至△ABF'的位置（點F對應點F'），

則△ADF≌△ABF'，∴BF'=DF，AF=AF'，

∠DAF=∠BAF'，∴EF'=BE+BF'=BE+DF=EF，易證

△AEF≌△AEF'(SSS)

∴∠EAF'=∠EAF，從而∠EAF=∠BAE+∠DAF=45°。

由半角模型原命題，其他結論易證。

（其他方法如截長補短法、解析法等與原命題證明類似，不再贅述）①④→②③⑤

∵點A是△CEF的旁心（或EA、FA分別平分∠BEF、∠DFE），（註：條件若改為EA平分∠BEF或FA平分∠DFE亦可）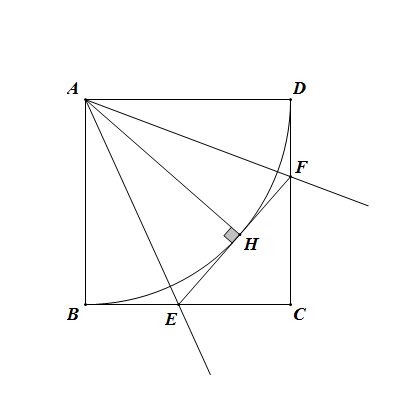

逆定理的證明（二）

且AB⊥BE，AH⊥HE，∴AB=AH，易證△ABE≌△AHE，

∴∠BAE=∠HAE；

同理可得∠DAF=∠HAF，

∴∠EAF= ∠BAD=45°

由半角模型原命題，其他結論易證。

（或根據切線長定理，證EF=BE+DF，從而得出結論亦可）

①⑤→②③④

根據角平分線定理的逆定理（或全等）可得∠EAF= ∠BAD=45°，由半角模型原命題，其他結論易證。

套用

半角模型是國中幾何方面問題的常見模型，常用於基本幾何命題的證明和一些邊長、角度等的計算。其逆定理則使其可用性更強，避免冗長的證明過程。

以下給出一些例題及答案，以供參考：