基本介紹
- 中文名:半線性變換
- 外文名:semilinear transformation
- 所屬學科:數學
- 屬性:線性變換的推廣
- 相關概念:半線性映射,線性變換,同構等
定義












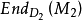
相關定理
命題1
定理1
定理2







命題2
定理3




















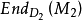














半線性變換(semilinear transformation)是線性變換的推廣。設V與V′分別是域P與P′上的線性空間,ρ為P與P′的同構,若V與V′的映射φ滿足條件:1.對任意α,β...
半線性映射(semi-linear mapping)是線性映射概念的推廣。線性映射亦稱同態或線性同態。線性代數的中心內容和基本概念之一。線性空間亦稱向量空間。它是線性代數的中心...
介紹 半單變換(semi-simple transformation)一類特殊的線性變換.設V是域P上的n維線性空間,。E HomP<V,V),若。恰有n個線性無關的特徵向量,則稱。為半單變換...
半線性單項式表示(semilinear monomial rep-resentation)群表示的一種類型.設V為域F上向量空間,(V,X, (Vs))為域F上單項式空間V的一切非奇異半線性變換構成一個...
線性代數是數學的一個分支,它的研究對象是向量,向量空間(或稱線性空間),線性變換和有限維的線性方程組。向量空間是現代數學的一個重要課題;因而,線性代數被廣泛地...
,若σ恰有n個線性無關的特徵向量,則稱σ為半單變換。半單變換關於基的矩陣是半單矩陣。線性變換σ為半單的充分必要條件是其最小多項式無重根。 [2] 半...
對於半賦范向量空間,可以定義類似的函式,這時E成為一個半度量空間(弱於度量空間...任意兩個有限維的賦范向量空間之間的線性變換也都是連續的。兩個賦范向量空間...
若環R的雅各布森根J(R)=0,則R稱為半本原環,又稱雅各布森半單環。一個環...上的稠密線性變換環。若環R 的理想 P 滿足 R/P 為左本原環,則稱 P 為 ...
線性變換環 Armendariz環 半交換環 矩陣環館藏號O153.3唯一標識符[1] 108.ndlc.2.1100009031010001/T3F24.003958961館藏目錄2009\O153.3\6參考資料 1. 矩陣...
設V是域P上的n維線性空間,σ∈HomP(V,V),若σ恰有n個線性無關的特徵向量,則稱σ為半單變換。半單變換關於基的矩陣是半單矩陣。線性變換σ為半單的充分...
一個把向量映射到非負實數的函式如果滿足簡介中描述的性質,就叫做一個半範數;...在賦范矢量空間之間的線性變換中,最重要的是連續線性變換,賦范矢量空間和連續...
