割點

在一個無向圖中，如果有一個頂點集合，刪除這個頂點集合以及這個集合中所有頂點相關聯的邊以後，圖的連通分量增多，就稱這個點集為割點集合。

如果某個割點集合只含有一個頂點X（也即{X}是一個割點集合），那么X稱為一個割點。

基本介紹

• 中文名：割點
• 外文名：cut-vertex
• 所屬領域：離散數學
• 相關概念：割點集、連通分支數、連通圖等
• 作者：王義和
• 定義：刪除這個頂點集合以所有頂點相關聯的邊以後，圖的連通分量增多

定義

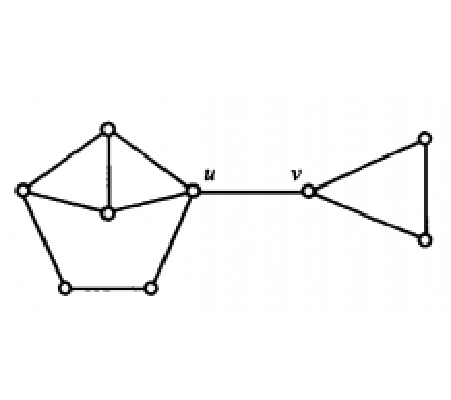
在無向聯通圖 G=(V,E)中: 若對於x∈V， 從圖中刪去節點x以及所有與x關聯的邊之後， G分裂成兩個或兩個以上不相連的子圖， 則稱x為G的割點。 簡而言之， 割點是無向聯通圖中的一個特殊的點， 刪去中這個點後， 此圖不再聯通， 而所以滿足這個條件的點所構成的集合即為割點集合。

設G是一個圖，x是G的一條邊，如果G-x的連通分支數大於G的連通分支數，則稱x是G的一個橋，或割邊。

圖1中，頂點u和v都是割點，其他頂點都不是割點，邊uv是橋，其他邊都不是橋。

圖1

對於鐵路和公路等交通圖，割點和橋在軍事、經濟上有重要的意義。顯然有割點的圖不是哈密頓圖。而如果uv是橋且deg(u)≥2，則u是一個割點。

相關性質

定理1

設v是連通圖的一個頂點，則下列命題等價：

(1)v是G的一個割點；

(2)存在與v不同的兩個頂點u和w，使得v在u與w間的每條路上；

(3)存在V\{v}的一個2-劃分，使得，v在u與w間的每條路上。

證明 (1)(3)：設是的一個割點，則的連通分支數大於G的連通分支數，於是至少有兩個連通分支。令U是G-v的一個連通分支的頂點集，W是其他各連通分支構成的的子圖的頂點集。

顯然是V\{v}的一個2-劃分。對，u與w不在的同一個連通分支中，所以在中u與w間沒有路。而因為G是連通圖，所以在G中u與w間有路。因此，在G中，v必在u與w間的每條路上。

(3)(2)：(2)是(3)的特例，所以(3)成立時(2)必成立。

(2)(1)：假設(2)成立，欲證(1)成立，只需證是不連通圖。用反證法。假設連通，則在中至少有一條u與w間的路。於是G中有一條不過v的u與w間的路，這與(2)矛盾。所以是不連通圖，從而v是G的一個割點。

定理2

每個非平凡的連通圖中至少有兩個頂點不是割點。

證明 每個非平凡的連通圖必有生成樹，非平凡的樹至少有兩個度數為1的頂點，它們就不是非平凡的連通圖的割點。

定理3

設x為連通圖的邊，則下列命題等價：

(1)x是G的橋；

(2)x不在G的任一圈上；

(3)存在兩個不同的頂點u和w，使得x在每一條u與w間的每條路上；

(4)存在V的一個2-劃分，使得，x在u與w間的每條路上。