分歧指數

分歧指數(ramification index)是在域擴張時，素除子延拓或素理想分解的指數。域擴張是域論的基本概念之一。若域K包含域F作為它的子域，則稱K是F的一個擴張(或擴域)，F稱為基域，常記為K/F。此時，K可以看成F上的向量空間。研究擴域K(相對於基域F)的代數性質，是域論研究的一個基本內容。

基本介紹

• 外文名：ramification index
• 領域：數學
• 學科：域論
• 概念：素除子延拓或素理想分解的指數
• 對象：非阿基米德素除子

概念

分歧指數(ramification index)是在域擴張時，素除子延拓或素理想分解的指數。若P為域F的非阿基米德素除子，Q為P在擴域E中的延拓，w和v是Q及P相應的指數賦值，則：

稱為Q對P的分歧指數。若F對離散的P是完備的，n=[E∶F]有限，則e(Q/P)f(Q/P)=n，式中f(Q/P)為剩餘類次數。

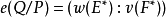
域擴張

域論的基本概念之一。若域K包含域F作為它的子域，則稱K是F的一個擴張(或擴域)，F稱為基域，常記為K/F。此時，K可以看成F上的向量空間。研究擴域K(相對於基域F)的代數性質，是域論研究的一個基本內容。

若域E是F的擴域，K是E的擴域，則稱E是域擴張K/F的中間域。若K/F是域擴張，S是K的子集，且F(S)是K的含F與S的最小子域，稱F(S)為F添加S的擴域。當S={α₁，α₂，…，α_n}是有限集合時，F(α₁，α₂，…，α_n)稱為添加α₁，α₂，…，α_n於F的有限生成擴域(或者F上的有限生成擴張)。它由一切形如f(α₁，α₂，…，α_n)/g(α₁，α₂，…，α_n)的元組成，其中α₁，α₂，…，α_n∈S，f，g是F上的n元多項式且g(α₁，α₂，…，α_n)≠0。

由於這個原因，當F(α₁，α₂，…，α_n)關於F的超越次數≥1時，F(α₁，α₂，…，α_n)也稱為F上的代數函式域。當S={α}時，稱F(α)為F的單擴張域，也稱本原擴域。F的有限代數擴域K是單擴域的充分必要條件是，擴域K與基域間存在有限箇中間域。這是施泰尼茨(Steinitz，E.)證明的。

域論

域論（Field Theory）是抽象代數的分支，是不少學科的基礎，是代數學中最基本的概念之一，且歷史悠久。研究域的性質，簡單地說，一個域是在其上有"加法"、"減法"、"乘法"和"除法"的代數結構。

域是許多數學分支(如代數、代數數論、代數幾何等)研究的基礎，而有限域則在近代編碼、正交試驗設計和計算機理論中都有重要套用，通過理想來研究環，這是研究環的基本方法。但是，由於域只有平凡理想，因此無法通過域的理想來研究域，要研究域，必須採取別的方法，其中最基本的方法就是通過對域添加若干元進行擴張，域的擴張起源於數域的擴張。

早在19世紀初，伽羅華在研究代數方程的著作里就出現了域的概念的萌芽，後來戴德金(J.W.R.Dedekind)和克羅內克(L.Kronecker)在不同背景下也提出了域的概念。系統研究域的理論始於韋伯(H.Weber)，而域的公理系統是迪克森(L.E.Dickson)和亨廷頓(E.V.Huntington)分別於1903和1905年獨立創立的。在韋伯等人的影響下，施泰尼茨(E.Steinitz)對抽象域進行了系統研究，於1910年發表論文“域的代數理論”，對域論本身以及相關科學的發展產生重大影響。

域的概念最初被阿貝爾和伽羅瓦隱含地用於他們各自對方程的可解性的工作上。

1871年，理察·戴德金將對於四則運算封閉的實數或複數集稱為“域”。

1881年，利奧波德·克羅內克定義了“有理域”（英文：domain of rationality，德文：Rationalitäts-Bereich），相當於今稱之數域。

1893年，安里西·韋伯給出抽象域的首個清晰定義。

1910年，施泰尼茨於1911年發表了論文《域的代數理論》（英文：Algebraic Theory of Fields、德文：Algebraische Theorie der Körper）。論文中他以公理化的方式研究了域的性質並給出了多個域的有關術語，比如素域、完全域，和域擴張的超越次數。

雖然伽羅瓦並未提出域的概念，但一般被譽為是首個將群論和域論連繫起來的數學家，伽羅瓦理論便以他命名。事實上，埃米爾·阿廷在1928至42年間才將群和域的關係大大地發展。

除子

亦稱韋伊除子。是研究代數簇的重要工具之一。不可約簇X上余維數為1的不可約子簇的代數和。具體地，若D表示X中不含於X的奇異軌跡之中且余維數為1的不可約子簇的全體，Div(X)表示以D為基的自由阿貝爾群，則Div(X)中的元稱為除子。設A=∑n_iA_i是一個除子，A_i是不可約子簇，若所有的n_i≥0，則稱A為有效除子，稱A_i為素除子。例如，若X是余維數1正則的(即X的所有一維局部環都是正則環)射影簇，A是X上的素除子，則O_A是一個離散賦值環。若f是X上的非零有理函式，則對O_A的賦值v_A，v_A(f)是個整數，且除了有限多個A之外，v_A(f)=0。因此，可以定義f的除子：

這種除子稱為主除子。若兩個除子D，D′的差等於一個主除子，即D-D′=div(f)，則稱D和D′是線性等價的。Div(X)關於線性等價的商群稱為X的除子類群，記為Cl(X)。

素除子

一個賦值等價類。兩個賦值等價若且唯若其決定的拓撲相同，也若且唯若其中一個賦值是另一賦值的冪。由此得到的賦值等價類稱為素除子。

理想

集合論中的基本概念之一。設S為任意集合，若I⊆P(S)且滿足：

1.∅∈I;

2.若X，Y∈I，則X∪Y∈I;

3.若X，Y⊆S，X∈I，Y⊆X，則Y∈I;

則稱I為集合S上的理想。理想的概念在現代數學的幾乎每個分支中均有套用，且有許多變體或引申。例如，布爾代數上的理想即為集合上的理想的一種變體。設B為任意布爾代數，若B的一個子集I滿足：

1.0∈I，1∉I(其中0，1分別為布爾代數B中的零元與么元)；

2.對任何u∈I，v∈I，有u+v∈I；

3.對任何u，v∈B，若u∈I且v≤u，又v∈I；

則稱I為B上的理想。理想與濾子有非常密切的聯繫。

素理想

一類特殊理想。它是整數環中素數生成理想的推廣。設P是環R的理想，對R中任意理想A，B，若ABP必有AP或BP，則稱P為R的素理想。它等價於對x，y∈R，若xRyP則x∈P或y∈P。當R是交換環時，P是R的素理想若且唯若對R中任意元素a，b，若ab∈P，則a∈P或b∈P。素理想在交換環的理想理論中有重要作用。若對任意環R，a，b∈R，由ab∈P得出a∈P或b∈P，則稱P為R的完全素理想。因此，對交換環來說，素與完全素概念是一致的。