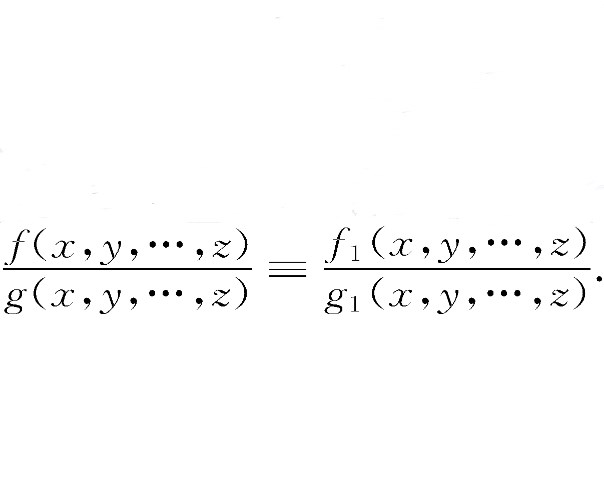分式恆等式(identity of fractions)是一種特殊的恆等式。如果對於變數的一切允許值,等式f(x,y,…,z)·g1(x,y,…,z)=f1(x,y,…,z)·g(x,y,…,z)成立,那么稱兩個分式f(x,y,…,z)/g(x,y,…,z)與f1(x,y,…,z)/g1(x,y,…,z)恆等。
基本介紹
- 中文名:分式恆等式
- 外文名:identity of fractions
- 所屬學科:數學
- 所屬問題:初等代數(代數式)
基本介紹,分式恆等式的證明,
基本介紹
兩個代數分式


若對於所有(已知數域內)自變數值,均使恆等式PQ1≡P1Q成立,則稱這兩個代數分式為恆等的,即

任何代數分式P(x,y,…,z)/Q(x,y,…,z)都有和它恆等的既約分式p(x,y,…,z)/q(x,y,…,z)≡P(x,y,…,z)/Q(x,y,…,z),除分子分母的(在所設數域內的)數值公因子外,這既約分式(即“最簡分式”)是唯一的。
分式恆等式的證明
分式恆等式的證明題,其證法常有:從左到右、從右到左、“左右開弓”(即證明左右兩邊都等於同一式子),還有求差法(即證明左邊-右邊=0)、求商法(即證左邊÷右邊=1)、反證法及等價命題法等,對於左邊複雜,右邊簡單,可考慮“從左到右”的證法;另外,對於一個含有未知數的等式,如果它不是方程(包括矛盾方程)那么它一定是恆等式(換句話說,就是:如果一個n次方程,有不只n個的未知數的值能使方程兩邊的值相等,那么它必是一個恆等式),此法稱為“反證法”。例如要證明恆等式

【例1】求證:

分析 


據此將原式變形後即可得證。
證明:左式=


【例2】求證:


分析 由



即可得證。
證明