歷史 克里金法的命名來自於南非金礦工程師丹尼·克里格(Danie G. Krige),以紀念其使用回歸方法對空間場進行預測的開創性研究。克里金法(普通克里金)的提出者為法國統計學家喬治斯·馬瑟倫(Georges Matheron),在其1963年發表的著作Principles of geostatistics中,馬瑟倫將克里金法定義為“對已知樣本加權平均以估計平面上的未知點,並使得估計值與真實值的數學期望相同且方差最小的地統計學過程”
(原文)“
... a geostatistical procedure called "kriging" ... consists in estimating the grade of a panel by computing the weighted average of available samples,..., we attempt to evaluate the unknown grade z of the panel with a linear estimator …
and must have the same average value within the whole large field … the (weights) have such values that estimation variance of by ,… should take the smallest possible value.” 馬瑟倫在提出克里金法的同時使用了BLUP理論,為克里金法的發展奠定了基礎。但在這一時期,不同領域的諸多研究都得到了等價或類似於克里金的估計方法。
在大氣科學領域,前蘇聯氣象學家列夫·舍米諾維奇·加丁(Лев Семено́вич Гандин)在其1963年發表的著作“氣象場的客觀分析(Objective analysis of meteorological field)”中開展了與馬瑟倫相同的工作。在該著作1965年的英語譯本中,簡單克里金被稱為“最優插值(optimum interpolation)”、普通克里金被稱為“歸一化權重最優插值(optimum interpolation with normalization of weighting fuctors )”、協同克里金被稱為“最優空間場匹配(optimum matching of flelds)”。加丁在其著作中同樣發展了克里金法的BLUP理論並討論了克里金法在氣象領域的套用。
在
高斯過程 領域,
安德雷·柯爾莫哥洛夫 (Андрей Николаевич Колмогоров)和羅伯特·維納(Robert Wiener)在二十世紀40年代開展了包括線性預測和BLUP理論在內的工作,並將其套用於
時間序列 數據中,被後世稱為維納-柯爾莫哥洛夫濾波器(Wiener-Kolmogorov filter)的信號處理技術是與克里金法十分接近的求解系統。隨後在70年代,高斯過程理論和貝葉斯推斷被逐步套用於空間場的研究,促進了克里金法的發展。
理論 固有平穩過程 克里金法在對空間場進行預測時,將空間場視為
隨機過程 (stochastic process)的推廣,即隨機場(random field)。具體而言,若對指數集
有隨機過程
且
為一
拓撲空間 (topological space),則
被稱為隨機場。克里金法中隨機場所對應的指數集通常為
地理坐標 ,而隨機場內每一個點的
測度 都是一個
隨機變數 ,服從特定的機率分布。
根據
地理學第一定律 (the first law of geography),地理空間上的所有值都是互相聯繫的,且距離近的值具有更強的聯繫。隨機場使用
協方差函式 對上述結論進行刻畫,對應高斯過程回歸(GPR)理論中的“
核函式 (kernel function)”。使用克里金法需要隨機場滿足兩個假設:
對隨機場內任意兩點,其協方差函式僅是點間向量的函式。
滿足上述假設的隨機過程被稱為固有平穩過程(intrinsically stationary process),二階平穩過程(second-order stationary process)是其特例。平穩高斯過程不僅是嚴格的平穩過程,而且在許多問題中是一個理由充分的假設,因此克里金法有部分研究完全基於高斯隨機場展開。
克里金法通常假設固有平穩過程是
各向同性 (isotropy)的,即其協方差函式僅是點間
歐氏距離 (Euclidean distance)的函式。各向同性隨機場可以直接使用
變異函式 (variogram)進行建模,簡化了克里金法的求解步驟。此外,一些特定類型的各項異性,例如幾何各向異性(geometric anisotropy)可以通過坐標變換轉化為各向同性。
類似於高斯過程回歸,克里金法不要求樣本服從特定的機率分布,但實踐中當樣本沒有偏斜數據時,克里金法往往有好的效果。
BLUP 克里金法是對已知函式進行加權平均估計未知函式的方法,其預測理論接近於
線性回歸 ,因此也有類似高斯-馬爾可夫定理(Gauss-Markov theorem)的
BLUP 理論。
將隨機場中變數的估計表示為包含
隨機誤差 的
線性系統 ,則BLUP可表示為選擇線性系統參數使估計值
和真實值
的
方差 最小:
式中
為未知點,
為隨機場的樣本,
為權重係數,通常被稱為克里金權重(Kriging weights)。由方差定義可知,當估計值和真實值的
數學期望 相同時,兩者的方差最小:
使用上述BLUP條件求解的權重係數
包含樣本點與未知點間的
協方差函式 (或
變異函式 ),因此只有隨機場的協方差函式已知,或隨機場為固有平穩過程時,克里金法才能給出BLUP。
算法 普通克里金 普通克里金(Ordinary Kriging, OK)是最早被提出和系統研究的克里金法,並隨著地統計學的發展衍生出一系列變體和改進算法。普通克里金是一個線性估計系統,適用於任何滿足各向同性假設的固有平穩隨機場。
各向同性假設下的固有平穩隨機場中,數學期望
與其位置無關,且協方差僅是點間距離
的函式。通常隨機場的協方差函式
是未知的,需要使用
變異函式 作為近似,此時變異函式
也僅與點間距離有關:
定義
為n個樣本
的對應值,則普通克里金問題和克里金方差有如下表示:
式中
是
在未知點
處的估計,
是點
和
間的協方差函式。由BLUP理論易證明普通克里金的無偏估計條件是所有權重係數之和為1:
。由此可使用
拉格朗日乘數法 構造如下求解函式並得到普通克里金問題的方程組:
該方程組有時也被稱為普通克里金系統(ordinary Kriging system),包含n+1個方程以求解n個權重係數。常見的求解方式是將克里金系統寫為矩陣形式並對矩陣求逆。求解後以矩陣形式表示的克里金權重為:
式中
為協方差矩陣,
為未知點和樣本間協方差組成的列向量,
為n個1組成的列向量。將所得權重帶入先前公式中可以得到普通克里金的無偏估計
:
由上式易知,隨機場的數學期望為
。若隨機場的數學期望已知(通常假設為0),則普通克里金退化為簡單克里金(simple Kriging)。由於固有平穩隨機場的數學期望處處相等,因此簡單克里金自身滿足BLUP條件,容易解得其克里金權重為
。
在高斯隨機場中,普通克里金和簡單克里金的估計值有如下分布的
置信區間:
改進算法 泛克里金(Universal Kriging, UK)
在已知隨機場是各項同性的固有平穩過程和漂移量(drift)的疊加時,可以使用泛克里金對隨機場進行建模。泛克里金假設漂移量是一系列已知解析函式
的
線性組合 :
式中
是隨機場的漂移,
是滿足各向同性假設的固有平穩隨機場。最常見的漂移是
線性函式 ,對應具有線性趨勢的隨機場。泛克里金的問題表述和克里金方差與普通克里金相同,其無偏估計條件有如下表述:
當
且
時,泛克里金與普通克里金的無偏估計條件等價,因此普通克里金可以視為泛克里金的一個特例。將上式作為拉格朗日乘子可得泛克里金的求解系統:
將求解所的權重帶入先前公式中可以得到泛克里金在
的估計值
。在高斯隨機場中,泛克里金和普通克里金以相同的方法估計置信區間。
協同克里金(Co-Kriging, CK)
協同克里金是克里金法在處理多變數問題時的改進,其中需要建模的隨機場稱為主變數,參與建模的其它隨機場稱為協變數。協同克里金可以有任意個數的協變數,但主變數和協變數必須具有
相關性 (correlation)且均是滿足各向同性假設的固有平穩隨機場。協同克里金可以使用互變異函式(cross-covariogram)估計隨機場間的
互協方差函式 (cross-covariance),但要求後者是對稱的,即
。
若主變數
擁有M個協變數
且每個變數擁有
個樣本,則協同克里金的最佳化問題和克里金方差有如下表示:
式中
為主變數的協方差函式,
為主變數與協變數間的互協方差函式。協同克里金的無偏估計條件為主變數權重係數之和為1,協變數權重係數之和為0:
類似普通克里金法,使用拉格朗日乘數法可以構造協同克里金系統求解係數
:
上述算法為基於普通克里金髮展的協同克里金,泛克里金也有對應的協同算法,被稱為“泛協同克里金(universal co-Kriging)”。協同克里金和泛協同克里金通常要求協變數擁有充足的樣本。若協變數的樣本量不足以計算互變異函式。可計算偽互變異函式(pseudo cross-variogram)作為近似。
析取克里金(Disjunctive Kriging, DK)
普通克里金是隨機場的BLUP,但在隨機場和指數集之間存在非線性關係時,線性估計結果往往不是最優的。析取克里金將普通克里金中的權重係數推廣為函式,從而實現了對隨機場的非線性估計。析取克里金可以定義為如下的最佳化問題:
式中函式
為預先給定的非線性函式。最常見地,給定
指示函式 時,析取克里金又被稱為指示克里金(Indicator Kriging, IK)。析取克里金求解給定函式使得
成為真實值
在由
構成的向量空間中的
正交投影 ,由此可得其問題表述為:
析取克里金要求樣本集是同因子的(isofactorial),但套用中通常直接假設樣本集服從聯合常態分配,此時使用
階
埃爾米特多項式 (Hermite polynomial)對函式
進行展開可將上式轉化為:
式中
為k階埃爾米特多項式,
為滿足如下關係的待定參數:
由埃爾米特多展開後的析取克里金問題,可得其克里金方差為:
析取克里金在每個埃爾米特展開上使用普通克里金求解
和
具體的求解過程依賴於
數值計算 ,考慮計算的複雜程度,通常將埃爾米特展開級數限制在100以內。
混合算法 回歸克里金(regression-Kriging)
回歸克里金是
廣義線性模型 (Generalized Linear Model, GLM)和克里金法相結合的算法,也是最常見的混合算法。回歸克里金首先使用GLM估計空間場中的系統性效應(determinstic effect),隨後使用克里金法估計由回歸
殘差 構成的隨機場:
回歸克里金考慮了空間場的趨勢,因此和泛克里金較為相似,但後者是基於隨機場假設的空間估計,而回歸克里金則將線性趨勢和隨機過程完全分開。
神經網路克里金(neural Kriging)
神經網路克里金可見於大氣科學研究中,一些文獻也將其稱為“直接神經網路殘差克里金(Direct Neural Network Residual Kriging, DNNRK)”。神經網路克里金與回歸克里金在邏輯上類似,即首先使用各類
人工神經網路 (Artificial Neural Network, ANN)算法對空間場進行建模,隨後使用克里金法估計殘差。
神經網路克里金,ANN輸出(左),克里金殘差(右),組合(下) 貝葉斯克里金(Bayesian Kriging)
貝葉斯克里金是使用
貝葉斯推斷 (Bayesian inference)的克里金法的統稱。貝葉斯克里金使用由
超參數 (hyper-parameter)的
先驗 (prior)定義克里金系統的參數(權重係數)並估計其
後驗 (posterior)。貝葉斯克里金的先驗通常為
常態分配 和
Gamma分布 。
常見的貝葉斯克里金框架包括Kitanidis算法和Handcock算法。其中Kitanidis算法要求隨機場的協方差除尺度外已知
,在實際套用中難以滿足;Handcock算法不要求協方差函式已知,而是將其表示為馬頓核(Matérn kernel)形式的高斯過程先驗並使用極大似然估計(Maximum Likelihood Estimation, MLE)求解超參數。兩種算法都以高斯隨機場為前提,且後者是與高斯過程回歸等價的方法。對非高斯隨機場,Handcock算法有貝葉斯高斯變換(Bayesian Transformed Gaussian, BTG)算法。而對更一般的
各向異性 隨機場,以及有同時包含空間和時間觀測樣本的情形,可以使用等級貝葉斯克里金(hierarchical bayesian Kriging)。該方法可以對非平穩隨機場使用,其中協方差函式完全由超參數進行模擬。
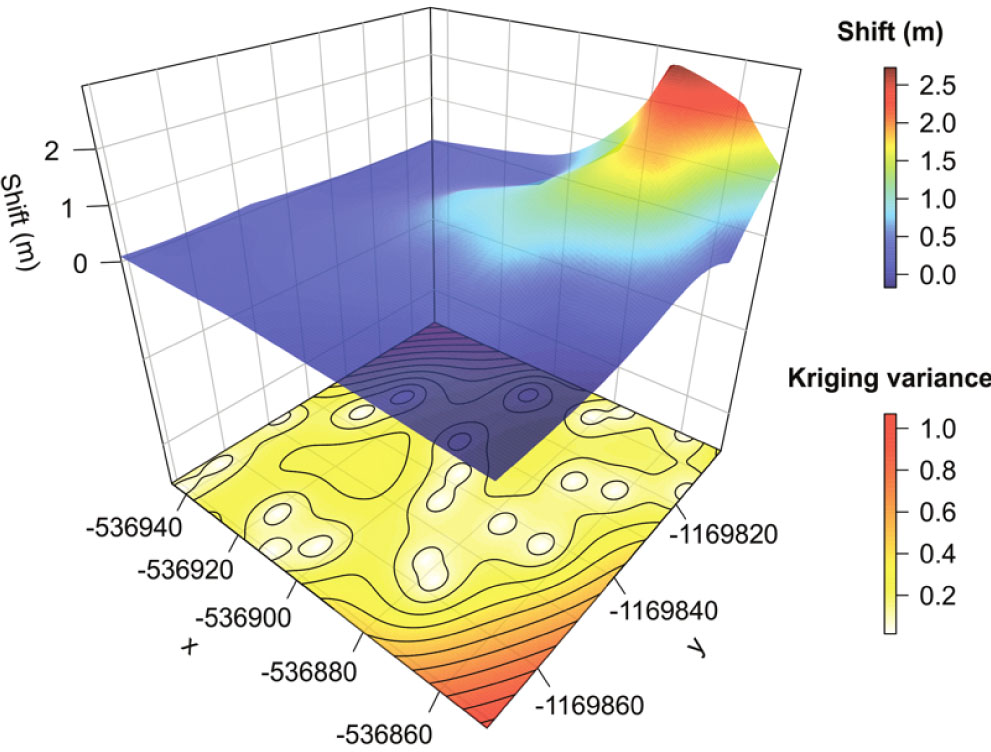
性質 克里金法是一個確切估計器(exact estimator),由克里金法的求解系統可知,其估計的隨機場在樣本點的取值與對應觀測值一致。這一性質的優勢在於克里金法的估計總是與觀測值接近,不會與實際情況相距太遠;但估計值總是介於觀測值之間,不能模擬劇烈的的變化。
由於克里金法在套用中使用擬合經驗變異函式的方式估計隨機場的協方差,而變異函式模型除塊金(原點)外都是
連續函式 ,因此克里金法對隨機場的估計是平滑的。這意味著在偏斜樣本中克里金法對異常值敏感,因此對偏斜樣本進行正態變換,例如
Box-Cox變換 是常見的做法。
克里金法僅在隨機場為固有平穩過程時提供BLUP,因此在使用克里金法前有必要通過樣本考察隨機場的穩定性,一個常見的方法是繪製
沃羅諾伊圖 (Voronoi diagram),計算標準差並觀察是否有局地異常值。
在克里金法中,所有樣本都會參與對未知點的估計,且在
變異函式 隨距離遞增的情形下,與未知點距離近的樣本影響更大。實際套用中為突出隨機場的局地特徵,可以人為設定點的影響範圍,不考慮範圍外樣本的影響。這一性質也意味著若隨機場某處沒有臨近的樣本,則其克里金方差會增大,因此克里金法僅適用於格點數據的內插值。普通克里金的外插結果隨點距離的增大趨近於樣本平均值;泛克里金會在外插時將漂移量無限外推。
與
高斯過程回歸 (GPR)的關係:GPR是與克里金法相近的非參數模型,常見於機器學習領域。若協方差函式的形式等價,簡單克里金和普通克里金的輸出與GPR在正態似然下輸出的數學期望相同。GPR與克里金法的不同點在於,前者假設隨機場為高斯過程並給出其對測試樣本後驗的完整分布;後者假設隨機場為固有平穩過程並給出其對測試樣本的最優無偏估計。此外,一些貝葉斯克里金方法,例如Handcock算法與GPR是等價的,可參見Handock and Stein (1993)。
套用 克里金法被廣泛用於各類觀測的空間插值,例如地質學中的
地下水位 和
土壤濕度 的採樣;環境科學研究中的大氣污染(例如
臭氧 )和土壤污染物的研究;以及大氣科學中的近地面
風場 、
氣溫 、
降水 等的單點觀測。
克里金法在工程問題的數值試驗中可作為
代理模型 (surrogate model)對有限的模擬結果進行插值。具體而言,若對問題全局使用
確定性模擬方法 (deterministic computer simulations),例如
有限元方法 會占用大量計算資源而無法(快速)實現時,可以僅模擬局部個別點的結果並使用克里金法插值到全局。
包含克里金法的編程模組
作為一種典型的地統計學算法,克里金法被廣泛收錄於各類代碼庫中,以下對其進行部分歸納:
語言
代碼庫
OK
UK
CK
IK/DK
說明
gstat
可用
可用
可用
可用
包含偏斜數據處理、變異函式分析、各向異性建模和交叉驗證模組
geoR
可用
可用
不可用
不可用
帶有貝葉斯參數估計
RandomField
可用
可用
可用
不可用
包含自定義克里金函式接口
mGstat
可用
可用
可用
可用
與R語言下的gstat類似
ooDACE
可用
可用
可用
不可用
帶有回歸克里金算法,包含變異函式分析、交叉驗證、誤差診斷模組
PyKrige
可用
可用
不可用
不可用
無
pyKriging
可用
可用
不可用
不可用
無
可用
可用
可用
可用
商用軟體,具有圖形界面,包含所有常用模組,帶有貝葉斯參數估計





















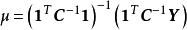












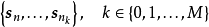


























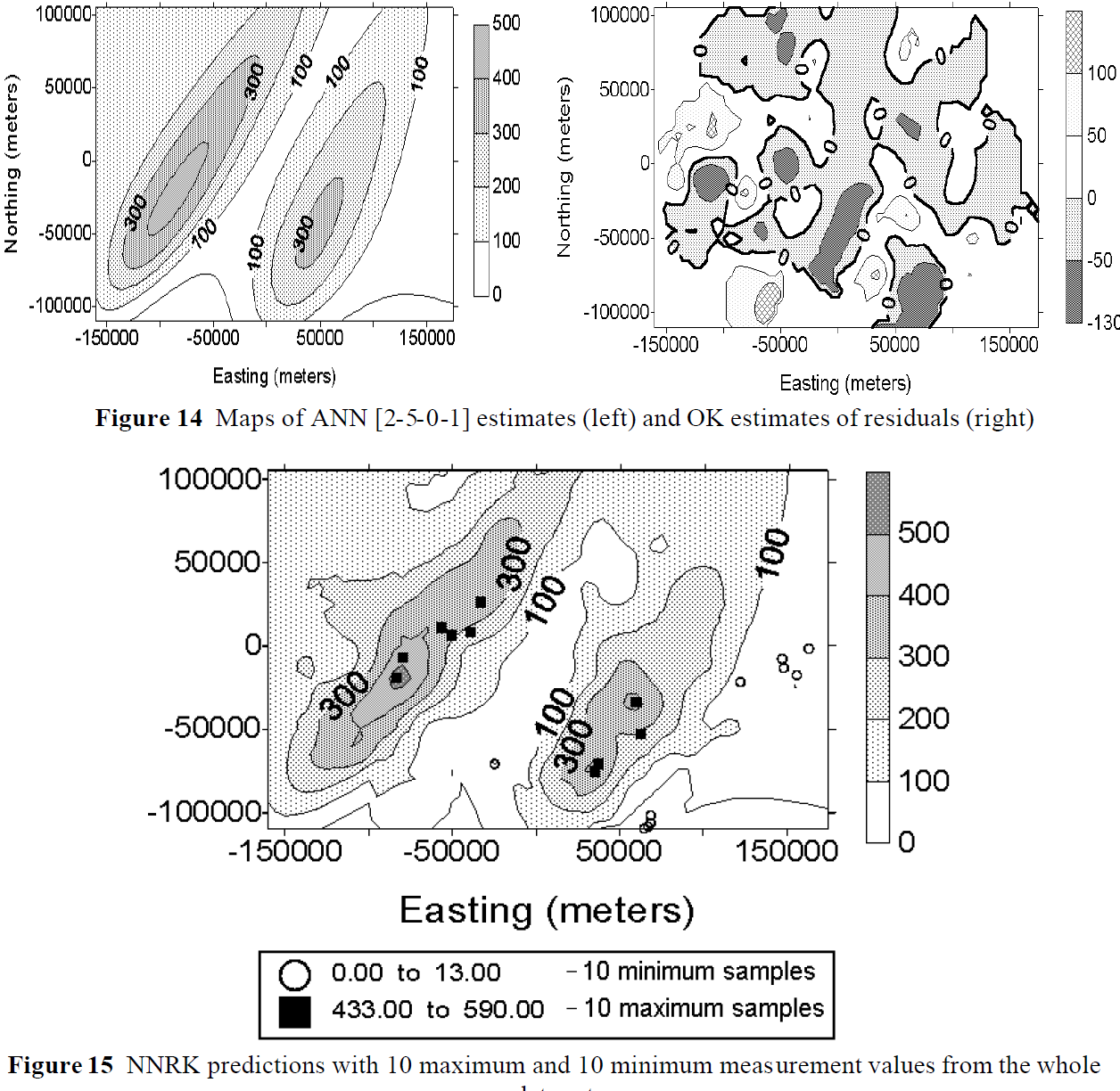 神經網路克里金,ANN輸出(左),克里金殘差(右),組合(下)
神經網路克里金,ANN輸出(左),克里金殘差(右),組合(下)