基本介紹
- 中文名:克萊茵曲面
- 外文名:Klein bottle
- 所屬學科:數學
- 所屬問題:拓撲學
- 別名:克萊茵壺、克萊茵瓶
- 屬性:一種單側曲面
- 提出者:德國數學家克萊因
- 提出時間:1882年
基本介紹,相關知識介紹,
基本介紹
在三維空間克萊茵曲面可以由一個兩端開口的管子(圖1)來構成,讓管子較細的一端穿過管壁,再讓管子兩端接合即可(圖2)。
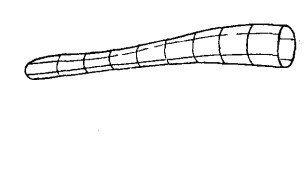 圖1
圖1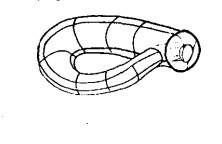 圖2
圖2克萊因瓶(Klein bottle)是德國數學家克萊因於1882年首先構造出的一個不能定向的閉曲面,是拓撲學中的著名例子。克萊茵瓶是將正方形的兩組對邊分別按下圖示箭頭方向迭合得到的閉曲面。從這構造方法可知,沿著它上面一條適當的閉曲線剪開,就成為牟比烏斯帶,因此它是不能定向的。除非自身相交,它不能嵌入3維歐氏空間,但可嵌人4維歐氏空間,如下圖是克萊因瓶的示意圖。
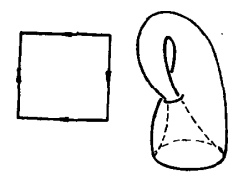 克萊因瓶
克萊因瓶相關知識介紹
幾何圖形在任何拓撲變換之下不變的性質叫作拓撲性質。拓撲學研究圖形的拓撲性質,不僅如此,它還研究幾何圖形的拓撲變換以及任意的連續變換。
下面這些都是拓撲性質:曲線或曲面的閉性質,閉曲線是簡單閉曲線的性質(也就是說,只含有一環),閉曲面被它上面任意閉曲線分割的性質(球面具有這個性質,而環面不具有這個性質),等等。
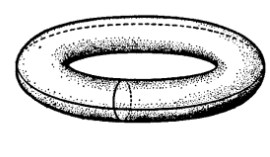 圖1
圖1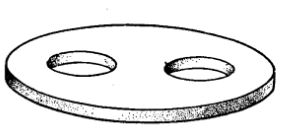 圖2
圖2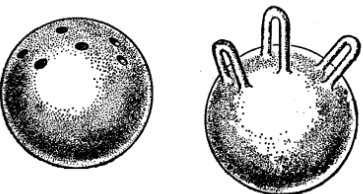 圖3
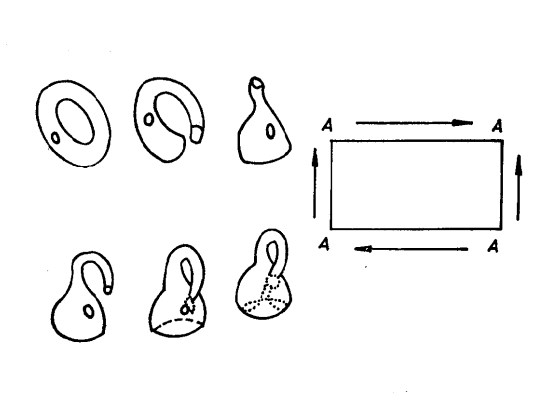
圖3在曲面上引閉曲線,使得把它們放在一起不組成曲面的劃分,也就是說,不把曲面分割為不連線的部分。在一個曲面上所能夠引的這樣的閉曲線的最大數目,叫作這個曲面的連通階。這個數目將使我們得到對於曲面拓撲結構的最重要的知識。我們可以看到,對於球面來說,它等於零(球面上的任何閉曲線組成劃分),在環面上可以找到兩條閉曲線,它們合起來還不致於分割環面,其中之一可取任意一條子午線,另一則取任意的平行環(圖1)。 但是在環面上不存在三條共同不分割這個曲面的閉曲線,環面的連通階等於2,像圖2里的麵包,它的表面就是一個連通階等於4的閉曲面,等等。一般地說,在一個球面上開2p個小圓洞(圖3上是p=3的情形),而把這些圓洞配為p對,在每一對上粘一個圓柱面(沿著邊粘),則得到一個手柄。 這樣我們就得到了一個帶有p個手柄的球面,或者叫作虧格為p的規範曲面,這個曲面的連通階等於2p。
用羅巴切夫斯基的說法,所有這些曲面都是空間的“截面”:它們每一個都把空間分為兩個區域,內部與外部,而它們自己是這兩個區域的公共邊界。這個性質又與另一個性質有關,那就是這些曲面當中的每一個都具有兩側:外側與內側(其中一側可以用一種顏色塗滿,而另一側則可用另一種顏色來塗)。
 圖4莫畢鄂斯帶子
圖4莫畢鄂斯帶子莫比烏斯帶
但是與這些曲面並存的還有所謂單側曲面,對它們來說無從區別兩側。最簡單的例子就是熟知的“莫畢鄂斯帶子”(即”莫比烏斯帶“)。把一個長方形紙條ABCD的AB邊與CD邊粘合,但粘時使頂點A合於頂點C,頂點B合於頂點D,我們就得到如同圖4所畫的曲面,它叫作莫畢鄂斯帶子。不難看出,在莫畢鄂斯帶子上不能區分兩側,不能用不同的顏色來塗滿兩個側面:沿著帶子的中線運行,從點E開始運行一周以後再回到點E時,雖然不曾經過帶子的邊界,但已到了與原來出發時不同的一側。 順便指出,莫畢鄂斯帶子的邊界是由單獨一條閉曲線所組成。
克萊茵曲面
於是產生了這樣的問題:是不是存在單側閉曲面,也就是說,不具有邊界的單側曲面?這種曲面是存在的,但如果把它們置放在三維空間裡,則必然會發生自己與自己相交的情況。典型的單側閉曲面的例子就如同圖5里所畫的,叫作“單側環面”或克萊茵曲面。 如果要避免自己交叉,構想把兩個莫畢鄂斯帶子沿著邊界粘合起來便得到克萊茵曲面(如同上面曾經提到過的,莫畢鄂斯帶子的邊界只含有一條周線)。
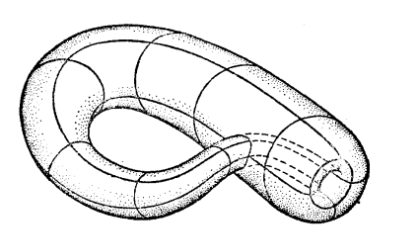 圖5
圖5現在我們可以來陳述曲面拓撲學的基本定理套用於雙側曲面的情形:任何一個雙側閉曲面必同胚於某個虧格為p的規範曲面,也就是“具有p個手柄的球面”。兩個雙側閉曲面同胚,若且唯若它們具有相同的虧格p(相同的連通階2p),也就是說,它們同胚於具有同樣多數目手柄的球面。
對於單側曲面來說,也有“規範形式”,類似於虧格p的雙側曲面所有的規範形式,但是比較難以表現出來,要得到這種規範形式,取一個球面來,在上面開p個圓洞,在每個洞上粘一個莫畢鄂斯帶子,使得帶子的邊界與圓洞口的邊界粘合,試圖作這種粘合時將碰到困難,因為根本不可能在空間裡具體地實現,在施行這樣的粘合時,必然又將導致曲面的自己交叉,而這種交叉是在空間裡實現單側閉曲面的模型時所不可避免的。
不能認為單側閉曲面只是數學裡的趣談,而與嚴肅的科學問題無關。要證實這種想法的錯誤,只需以射影幾何的產生為例證,這是幾何思想的一大成就,這門學科的原理現在已被列入大學或師範學院的課程中,射影幾何學的實際套用起源於配景理論,是在文藝復興時期(列昂納都·達·文西)由於建築、繪畫與技術製圖的需要而產生。射影幾何學最初一些定理的發現是十六——十七世紀的事,是由於純粹實用上的需要而產生,射影幾何的發展成為幾何學在純理論方面的一個最突出的推廣,特別,在它的基礎之上,人們初次徹底地理解了羅巴切夫斯基的非歐幾何學。
要從初等幾何里所討論的普通平面得到射影平面,只需在平面上補充一些抽象的元素,所謂非正常點或“無窮遠點”, 僅當作了這種補充以後,從一個平面到另一個平面的射影(從射影燈到銀幕的射影)才是從一個平面到另一個的一對一變換,把平面補充以非正常點,在解析幾何里就相當於從通常的笛卡兒坐標過渡到齊次坐標。也可以按照下述的方式來描寫:每一條直線補充了唯一的一個非正常點(“無窮遠點”);兩條直線具有相同的無窮遠點若且唯若它們是平行的,添加了唯一的無窮遠點以後,直線變成了閉曲線,而所有各直線上無窮遠點的全體按定義組成非正常的或無窮遠直線。
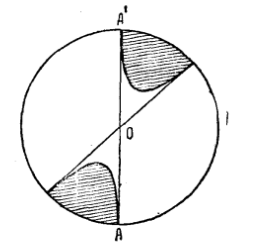 圖6
圖6因為平行的直線具有共同的無窮遠點,所以,要表達出在平面上補充無窮遠點的實際步驟,只需考慮通過平面上某個定點的直線,例如通過坐標原點O的直線(圖6),這些直線的無窮遠點已經把平面上所有的無窮遠點包羅無遺(因為每一條直線與通過點O的平行直線具有同一個無窮遠點)。因此,我們得到了射影平面的一個“模型”,這個模型是在一個以O為中心,具有“無窮大”半徑的圓里,把圓周上每一對對徑點(同一條直徑的兩個端點)粘合為直線AA’唯一的“無窮遠”點而得到的,整個圓周就變成了無窮遠直線,但這時必須記牢,圓周上的每一對對徑點是看作互相等同的一點的,由此立刻可以看出,射影平面是閉曲面,它沒有邊界。
如果在射影平面上考慮一條形狀如雙曲線(見圖6)的二次曲線,則很顯然這條雙曲線在射影平面上是一條閉曲線(只不過是被無窮遠直線分割成兩部分)。既然我們取作基本圓的圓周上每一對對徑點是粘合為一的,則不難看出,在圖6上用陰影表示的雙曲線內部同胚於普通的圓,而射影平面上沒有陰影的其餘部分則同胚於莫畢鄂斯帶子。因此,從拓撲的觀點來看,射影平面是把圓形(在我們的情形是雙曲線內部)與莫畢鄂斯帶子沿著邊界粘合以後所得的結果。 由這裡就立刻推知,射影幾何所研究的基本對象——射影平面,是一個單側的閉曲面。
除了極其重要的幾何意義以外,射影平面的有趣之點還在於它突出地表現了近代幾何思想的一個特點,這種特點是基於羅巴切夫斯基的發現而形成的,由於幾何圖形這個概念的特徵,幾何的思想總是抽象的。現在,它又進一步抽象化,如同我們所說的,在普通平面上補充進新的抽象元素——非正常點來,當然,這些抽象元素也反映了現實實際中的事物(每個“非正常點”不過就是一束平行直線的抽象化),但它們在我們的考慮中只是一種抽象的幾何元素,這種元素只能不完全地(不能予以物理實現地)用粘合某個圓周上對徑點後的結果來表示。在整個近代拓撲學裡,類似的抽象構造具有很大的價值,特別是當從曲面進入到三維或高維流形時,情況是如此。