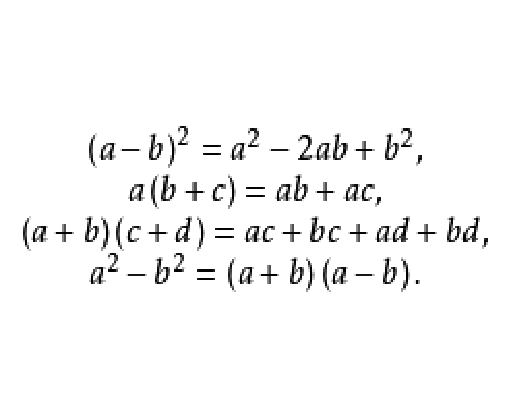如果兩個代數式A和B，對於它們中字母在允許範圍內任意取值，它們都有相同的值，那么就說這兩個代數式恆等。
基本介紹
- 中文名：代數恆等式
- 外文名：algebraic identity
- 所屬學科：數學（代數學）
- 相關概念：代數式
- 符號：A=B或A≡B
定義,代數式的恆等變形,恆等式的證明,恆等式舉例,幾何與代數恆等式,
定義
如果兩個代數式A和B，對於它們中字母在允許範圍內任意取值，它們都有相同的值，那么就說這兩個代數式恆等。
記作：
或
。如：
歐幾里得《原本》第二卷命題9的陳述是：
如果一直線被等分和不等分地劃分為兩部分，則以兩個不等部分為邊的二正方形之和，等於以直線的一半為邊的正方形加上以兩個分點間的線段為邊的正方形之和的兩倍。
從這個定理得到代數恆等式
代數式的恆等變形
把一個代數式變換成另一個與它恆等的代數式，就稱為代數式的恆等變形。
恆等式的證明
(1) 恆等式的證明，就是通過恆等變形，證明等號兩邊的代數式相等。
(2) 證明方法：①將左邊轉化為右邊或右邊轉化為左邊，一般從複雜向簡單的方向化解；②兩邊同時變形，化為相同代數式；③證明左邊-右邊=0或左邊/右邊=1且右邊≠0。
恆等式舉例
【例1】已知
，求證：
。
分析： ，證明等式實質就是證明等式左邊之和等於1，等式左邊的分母有兩個字母乘積，要用到已知條件，就必須轉化為
三項的乘積。
證明：左邊=
故等式成立。
【例2】已知
，求證：
。
分析：要證明左邊等於右邊，已知條件為 ，而求證式左右兩邊同時具備已知的部分條件，從而作差可以較好地證明。
證明：左邊-右邊
幾何與代數恆等式
由於古代希臘人完全是用長度表示數，根本沒有任何適當的代數符號。為了進行代數運算，他們設計了靈巧的幾何程式。這種幾何的代數，大部分被後人歸功於畢氏學派，並且在歐幾里得《原本》前幾卷中可以零星地見到。例如，《原本》第二卷有幾個命題實際上是以幾何術語表達的代數恆等式。看來，可以確信無疑，這些命題是古代畢氏學派用剖分法證明的。我們現在以第二卷中的幾何命題為例講講這種方法。
第二卷命題4，把邊長為
的正方形分成面積分別為
的兩個正方形和兩個矩形(圖1)，在幾何上證明代數恆等式
如果一條線段被分成兩部分，則以整個線段為邊的正方形等於分別以這兩部分為邊的正方形以及以這兩部分為邊的矩形的二倍之和。
圖1第二卷命題5的陳述是：
如果一線段既被等分又被不等分，則以不等分為邊的矩形加上以兩分點之間的線段為邊的正方形等於以這一線段的一半為邊的正方形。
令AB為給定的線段，並等分於P，不等分於Q，則此命題可寫作
圖2第二卷命題6的陳述是：
如果一線段被平分並被延長到任何一點，則以整個延長了的線段和其延長部分為邊的矩形加上以原線段的一半為邊的正方形，等於以由原線段的一半加上延長部分構成的線段為邊的正方形。
圖3在這裡(圖3)，如果給定的以P為中點的線段AB被延長到Q，則我們要證明的是
如圖4、5所示，令，提示恆等式
圖4
圖5