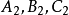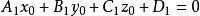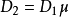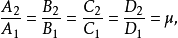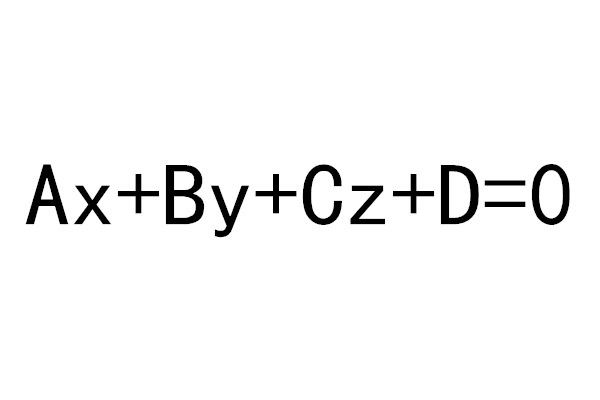一次曲面是曲面的一種,指方程是一次的曲面,在空間仿射坐標系中,三元一次方程Ax+By+Cz+D=0的圖形稱為一次曲面,一次曲面都是平面,每個平面的方程都是一次方程。
基本介紹
- 中文名:一次曲面
- 所屬學科:數學
- 所屬問題:空間解析幾何
- 簡介:三元一次方程Ax+By+Cz+D=0的圖形
基本介紹,平面是一次曲面,
基本介紹
在空間解析幾何中,空間曲面用三元方程F(x,y,z)=0來表示,如果方程中x,y,z都是一次的,所表示的曲面稱為一次曲面;同樣,二次方程所表示的曲面就稱為二次曲面。
平面是一次曲面
下面我們將確定一次曲面是平面,而且僅僅是平面,並且還要研究各種不同形式的平面方程式。
1.定理1 在笛卡兒直角坐標系中,每一個平面都是由一個一次方程式所確定的。
證明 設已知某笛卡兒直角坐標系,我們試研究任意平面α,並且證明這個平面是由一個一次方程式所確定的。在平面α上任取一點 ;此外再取垂直於平面α的任意向量(只要不等於零即可!)。我們用字母n表示這個向量,並用字母A, B, C表示它在坐標軸上的射影。
;此外再取垂直於平面α的任意向量(只要不等於零即可!)。我們用字母n表示這個向量,並用字母A, B, C表示它在坐標軸上的射影。

設M(x,y,z)是任意一點。當而且僅僅當向量 垂直於向量n時,該點才在平面α上。換句話說,M點在平面α上的條件是:
垂直於向量n時,該點才在平面α上。換句話說,M點在平面α上的條件是:


如果我們能用坐標x, y, z表示這個條件,那么,我們便得平面α的方程式。為了這個目的,我們寫出向量 和n的坐標:
和n的坐標:

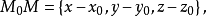
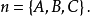
我們已知兩個向量互相垂直的判別法則,是它們的兩個對應坐標的乘積和等於零。因此,當而且僅僅當 的情況時,
的情況時, ⊥n。這就是我們所要求的平面α的方程式,因為當而且僅僅當M點在平面α上時(即當
⊥n。這就是我們所要求的平面α的方程式,因為當而且僅僅當M點在平面α上時(即當 ⊥n時),M點的坐標x, y,z才滿足此方程式。
⊥n時),M點的坐標x, y,z才滿足此方程式。



脫去括弧,將方程式(1)變形為:

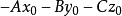
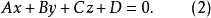
由此可知,平面α確實是由一個一次方程式所確定的。因此,定理得證。
2.凡垂直於平面的每一個向量(不等於零),都叫做它的法向量。使用這種命名,我們可以說:方程式


下列形式的方程式:
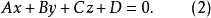
定理 在笛卡兒直角坐標系中每一個一次方程式確定一個平面。
證明 設已知任意一個笛卡兒直角坐標系,我們來研究任意一個一次方程式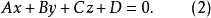 當我們說“任意”方程式時,那是說此時的係數A, B, C, D可以為任意數,當然要去掉三個係數A, B ,C同時都等於零的情況。我們必須證明方程式(2)是某平面的方程式。
當我們說“任意”方程式時,那是說此時的係數A, B, C, D可以為任意數,當然要去掉三個係數A, B ,C同時都等於零的情況。我們必須證明方程式(2)是某平面的方程式。
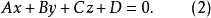
設 是方程式(2)的任意一組解,也就是三個解滿足這個方程式。用數
是方程式(2)的任意一組解,也就是三個解滿足這個方程式。用數 代換方程式(2)右邊的流動坐標,我們便得一算術恆等式:
代換方程式(2)右邊的流動坐標,我們便得一算術恆等式: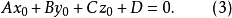


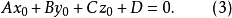
從方程式(2)減去恆等式(3),我們得方程式

根據上文所述(見2),它是通過點 且其法線向量為n={A,B,C}的平面方程式,但方程式(2)與方程式(1)是同解方程式,因為方程式(1是從方程式(2)減去恆等式(3)而得到的,而方程式(2),就本身而言,又是在方程式(1)加上恆等式(3)而得到的。所以,方程式(2)也是一個平面方程式。
且其法線向量為n={A,B,C}的平面方程式,但方程式(2)與方程式(1)是同解方程式,因為方程式(1是從方程式(2)減去恆等式(3)而得到的,而方程式(2),就本身而言,又是在方程式(1)加上恆等式(3)而得到的。所以,方程式(2)也是一個平面方程式。

我們既已證明,任意一個一次方程式確定一個平面,同時定理也就得到證明。
3.由笛卡兒坐標的一次方程式所確定的平面,我們知道叫做一次曲面。使用這個術語,我們可以將上述的結果敘述如下:
每一個平面是一個一次曲面,每一個一次曲面是一個平面。
4.如果兩個方程式 和
和 確定同一平面,則它們的係數成比例。
確定同一平面,則它們的係數成比例。


因為在這種情況下,向量 和
和 垂直於同一平面,所以它們彼此同方位。但這時候,數
垂直於同一平面,所以它們彼此同方位。但這時候,數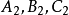 與數
與數 成比例;我們用μ表示這個比例乘數,便得:
成比例;我們用μ表示這個比例乘數,便得: 。設
。設 是平面上任意一點;它的坐標必須同時滿足這兩個方程式,因此,
是平面上任意一點;它的坐標必須同時滿足這兩個方程式,因此,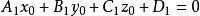 和
和 ,以μ乘第一個等式後,再減去第二個等式;我們便得:
,以μ乘第一個等式後,再減去第二個等式;我們便得: ,所以,
,所以,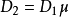 和
和