基本介紹
- 中文名:Burrows-Wheeler變換
- 外文名:Burrows-Wheeler Transformation
- 簡稱:BWT
- 也稱:BurrowsWheeler變換
- 定義:可逆的字元串順序變換
概述,Burrows–Wheeler變換過程,Burrows–Wheeler變換的逆過程,算法最佳化,基於 BWT 的無損壓縮,基於 BWT 的經典壓縮算法分析,前景與展望,
概述
Burrows–Wheeler變換(BWT,也稱作塊排序壓縮),是一個被套用在數據壓縮技術(如bzip2)中的算法。該算法於1994年被Michael Burrows和David Wheeler在位於加利福尼亞州帕洛阿爾托的DEC系統研究中心發明。它的基礎是之前Wheeler在1983年發明的一種沒有公開的轉換方法。
當一個字元串用該算法轉換時,算法只改變這個字元串中字元的順序而並不改變其字元。如果原字元串有幾個出現多次的子串,那么轉換過的字元串上就會有一些連續重複的字元,這對壓縮是很有用的。該方法能使得基於處理字元串中連續重複字元的技術(如MTF變換和遊程編碼)的編碼更容易被壓縮。
更加重要的是Burrows-Wheeler變換另一個特性,即在不儲存額外數據的前提下該變換是完全可逆的。換句話說,Burrows-Wheeler變換是一個“免費”的提高文本壓縮效率的算法,它以犧牲額外的計算為代價,換來的是更高效率的存儲壓縮。
舉個例子:
| 算法輸入 | SIX.MIXED.PIXIES.SIFT.SIXTY.PIXIE.DUST.BOXES |
|---|---|
| 算法輸出 | TEXYDST.E.IXIXIXXSSMPPS.B..E.S.EUSFXDIIOIIIT |
該算法的輸出因為有更多的重複字元而更容易被壓縮了。
擴展 Burrows-Wheeler 算法基本原理
設 D 為一個有序字母表,在 D 上定義一個有限字元序列(有時也稱為單詞) u = d1 d2…dn . 全部定義在 D 上的序列構成一個集合,記為 D* . 設a,b ∈D* ,如果存在 m,n ∈D* 使得 a = mn 以及b = mn ,則稱 a 是 b 的一個循環位移,也可稱 a 與b 是共軛的,記為 a ~ b . 若有 n ∈D* ,且 n =mkn = m,k = 1 ,則稱 n 為素詞. 因為 D 是一個有序的字母集合,所以在 D* 中任意兩個不同的單詞都可以按一定的順序比較先後,我們稱 D*為全序集合.設 m ∈D* ,令 mu = mmmm…,則 mu 是一個定義在 D 上的無限詞. 為判斷兩個無限詞的序關係,可採用字典順序. 假設給定兩個無限詞 α =α1α2α3… 以及 β = β1 β2 β3…,α < lexβ 意味著存在j 使得 αi = βi,i = 1,2,…,j - 1,且有 αj = βj.取定兩個素詞 p,q ∈D* ,其中 q Cp,利用Burrows-Wheeler 變換,分別得到 p,q 對應的共軛等價類 Cp 和 Cq . 易知,Cp ∩Cq = φ . 令 Sp,q = Cp ∪Cq . Sp,q 按照 < ω 序關係構成一個全序集. 用 0和 1 分別標記 Sp,q 中屬於 Cp 和 Cq 的元素.將 DNA 序列看成字母集 D = {A,C,G,T }上的一個詞.
Burrows–Wheeler變換過程
Burrows-Wheeler變換首先將輸入的序列進行“全循環排列”。即將輸入字元串的首位字母放置再最後一位,其他字母依次向前移動一位,得到原字元串一個循環排列字元串。重複循環排列的過程直至得到原始的字元串。此時可以得到全部可能的循環排列字元串,得到與字元數目相同的循環排列數目(如下表中有11個字母,得到11種可能的循環排列)。Burrows-Wheeler變換之後將得到的“全循環排列”的字元串按照字典序排序。排序後的每個全循環字元串的最後一個字母練成的字元串(即下表中“將所有的字元串按照字典序排序”中的最後一列),即為Burrows-Wheeler變換的輸出。
| Burrows–Wheeler變換過程 | |||||
|---|---|---|---|---|---|
abracadabra | 0 1 2 3 4 5 6 7 8 9 10 | a b r a c a d a b r a b r a c a d a b r a a r a c a d a b r a a b a c a d a b r a a b r c a d a b r a a b r a a d a b r a a b r a c d a b r a a b r a c a a b r a a b r a c a d b r a a b r a c a d a r a a b r a c a d a b a a b r a c a d a b r | a a b r a c a d a b r a b r a a b r a c a d a b r a c a d a b r a a c a d a b r a a b r a d a b r a a b r a c b r a a b r a c a d a b r a c a d a b r a a c a d a b r a a b r a d a b r a a b r a c a r a a b r a c a d a b r a c a d a b r a a b | 10 7 0 3 5 8 1 4 6 9 2 | rdarcaaaabb |
下面的偽代碼提供了一個樸素的算法過程,設s為輸入的字元串並以EOF為結尾:
function BWT (string s)
生成s所有的循環字元串
將這些字元串按字典序排序
返回最後排序後字元串的最後一列
Perl代碼實現:
#存入輸入序列@inputString = qw(a b r a c a d a b r a ); #構造全循環排列字元串#因為有字元數目相同的循環排列,所以循環11次for( $i = 0 ; $i <=11 ; $i ++ ){ $rotateStrings[$i] = join( "" , @inputString[ map( $_ - $i , 0 .. 10 ) ] );} #將全循環按照字典序排序@rotateIndex = sort { $rotateStrings[$a] cmp $rotateStrings[$b] } 0 .. 10 ; #取出每個排序後的循環排列字元串的最後一個字母,作為輸出foreach $_ ( @rotateIndex ){ $output .= substr($rotateStrings[$_],10,1);} #得到輸出結果:rdarcaaaabbprint "$output\n";Burrows–Wheeler變換的逆過程
Burrows-Wheeler變換最卓著的貢獻並不在於它能夠提供更加易於壓縮的輸出,而在於它提供了一種不需要額外數據就能夠實現可逆變換的算法。
逆變換的過程首先將原本的輸出放入一個列(加列1),然後對所有行進行字典序排序(排序1)。逆變換重複這一過程,在已經排序的結果前面加BWT的輸入的一列(加列2),然後再將所有行進行排序(排序2)。這一過程一直重複,直至每一行的字元數目與原本字元的數目相同為止。此時所有行就是原字元串的“全循環排列”的字元串。其中結尾為EOF的行,就是原本的字元串。(註:通常字元串的結尾以$表示)
加列1 | 排序1 | 加列2 | 排序2 | 加列3 | 排序3 | 加列4 | 排序4 |
r d a r c a a a a b b | a a a a a b b c d r r | ra da aa ra ca ab ab ac ad br br | aa ab ab ac ad br br ca da ra ra | raa dab aab rac cad abr abr aca ada bra bra | aab abr abr aca ada bra bra cad dab raa rac | raab dabr aabr raca cada abra abra acad adab braa brac | aabr abra abra acad adab braa brac cada dabr raab raca |
加列5 | 排序5 | 加列6 | 排序6 | 加列7 | 排序7 |
raabr dabra aabra racad cadab abraa abrac acada adabr braab braca | aabra abraa abrac acada adabr braab braca cadab dabra raabr racad | raabra dabraa aabrac racada cadabr abraab abraca acadab adabra braabr bracad | aabrac abraab abraca acadab adabra braabr bracad cadabr dabraa raabra racada | raabrac dabraab aabraca racadab cadabra abraabr abracad acadabr adabraa braabra bracada | aabraca abraabr abracad acadabr adabraa braabra bracada cadabra dabraab raabrac racadab |
加列8 | 排序8 | 加列9 | 排序9 |
raabraca dabraabr aabracad racadabr cadabraa abraabra abracada acadabra adabraab braabrac bracadab | aabracad abraabra abracada acadabra adabraab braabrac bracadab cadabraa dabraabr raabraca racadabr | raabracad dabraabra aabracada racadabra cadabraab abraabrac abracadab acadabraa adabraabr braabraca bracadabr | aabracada abraabrac abracadab acadabraa adabraabr braabraca bracadabr cadabraab dabraabra raabracad racadabra |
加列10 | 排序10 | 加列11 | 排序11 |
raabracada dabraabrac aabracadab racadabraa cadabraabr abraabraca abracadabr acadabraab adabraabra braabracad bracadabra | aabracadab abraabraca abracadabr acadabraab adabraabra braabracad bracadabra cadabraabr dabraabrac raabracada racadabraa | raabracadab dabraabraca aabracadabr racadabraab cadabraabra abraabracad abracadabra acadabraabr adabraabrac braabracada bracadabraa | aabracadabr abraabracad abracadabra acadabraabr adabraabrac braabracada bracadabraa cadabraabra dabraabraca raabracadab racadabraab |
下面的偽代碼提供了一個逆過程的樸素實現(輸入字元串s為原過程之輸出):
function inverseBWT (string s)
生成length(s)個空串a
循環 length(s) 次
將s放在串a的每一行的最前面一列
將a按照字典序排序
返回結尾為EOF的行
Perl代碼實現:
#輸入bwt的輸出結果@ibwtInput = qw(r d a r c a a a a b b); #Perl允許不聲明的構造空串for( $i = 0 ; $i <= 10 ; $i ++ ){ for( $j = 0 ; $j <= 10 ; $j ++){ #將bwt的結果放在串的每一個行的最前一列 $inverseStrings[$j] = $ibwtInput[$j].$inverseStrings[$j];}#將串進行字典序排序 @inverseStrings = sort {$a cmp $b} @inverseStrings;} #按照最後一位是EOF的結果輸出,通常用$標誌字元串結尾,這裡使用已知結果作為展示print $inverseStrings[2]."\n";算法最佳化
有許多關於Burrows-Wheeler變換算法的最佳化,可以在不改變輸出的前提下使得運算更加有效率。譬如在Burrows-Wheeler變換和Burrows-Wheeler逆變換過程中,都不需要循環的表。每一行的循環排序字元串可以用一個指向字元串的下標或指針表示,而排序的過程也用下標或指針進行。但是這裡要小心有的程式語言在用下標或指針進行排序時會不按照預想的方式工作,進而產生錯誤。
關於用下標最佳化Burrows-Wheeler變換的Perl代碼實現
@inputString=qw(a b r a c a d a b r a);@sortIndex = sort {join("",@inputString[$a..($a+$#inputString)]) cmp join("",@inputString[$b..($b+$#inputString)]) } 0..$#inputString;print join(",",@sortIndex)."\n".join("",@inputString[map($_-1,@sortIndex)])."\n";除此之外,其實可以通過下標或指針的方式記錄最後一位的字元,而不必加入EOF。這樣Burrows-Wheeler變換雖然輸出中新添了下標或指針 ,但是卻沒有了EOF,因此輸出的長度沒有明顯的增加。但是卻能夠節省計算。而Burrows-Wheeler逆變換則輸出沒有EOF的原始字元串。
基於 BWT 的無損壓縮
由於 BWT 能使大量相同的字元聚集在一起,使用 BWT 之後, 再對數據進行壓縮編碼, 可以獲得更好的壓縮效果。BWT 正在被廣泛研究與套用( 不僅用於壓縮, 還用於數據加密和壓縮域搜尋等) , 如開源壓縮工具 bzip 利用 BWT 獲得了巨大的成功, 傳統的基於 BWT 的無損壓縮系統結構如下圖 所示。
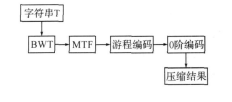 系統結構
系統結構系統結構MTF( Move-to-front) 的基本操作是輸出當前字元在字元集中的位置, 並把該字元移到字元集前端。由於 T 經 BWT 後, 會出現連續的相同字元,所以經 MTF 之後, 得到的結果將是連續的 0 和一些列的小整數, 利於進一步降低整體熵值。
遊程編碼( RLE: Run-Length encoding ) 是將具有相同數值的、連續出現的字元構成的字元串用數值及串的長度表示。0 階編碼一般採用算術編碼和 Huffman 編碼,如 bzip 使用的是算術編碼, 由於受專利限制, bzip2改用了 Huffman 編碼。
基於 BWT 的經典壓縮算法分析
經過前面的介紹和分析, 我們可以推測, 對數據經過 BWT 後再使用經典壓縮算法進行編碼, 將使壓縮效果進一步提高。由於 MTF 和遊程編碼只對連續出現的字元才能起到壓縮效果, 而對非連續但是存在上下文相關性的字元串反而會使編碼長度增加, 所以我們在此摒棄了這兩個環節, 多階算術編碼和 LZW 算法能有效的利用連續和非連續字元的相關性進行壓縮。在進行 BWT 時我們設定的數據塊大小為 2 兆位元組( MByte) , 用 BWT 進行完預處理, 再進行三階算術編碼和 LZW 編碼的試驗結果如下圖所示。
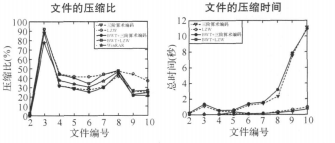 BWT算法分析
BWT算法分析從左圖可以看出, 小於 2 兆位元組的檔案, 其 BWT 前後壓縮比變化不明顯, 但大於 2 兆位元組的檔案( 檔案9 和檔案 10) , 進行 BWT 之後, 其壓縮比顯著下降,兩檔案在LZW 編碼下壓縮比分別降低了 18. 84%和11. 33%, 在三階算術編碼下分別降低了 5. 15%和2.83%。 還可知壓縮工具 WinRAR 對測試檔案的壓縮比介於三階算術編碼和 LZW 之間。從右圖可知,BWT 前後壓縮算法的總耗時沒有明顯的變化, 三階算術編碼略增, LZW 略減。通過以上分析可知, 對於較大的檔案, 經 BWT分塊排序再進行壓縮, 壓縮效果能有效提高。,所以 BWT 結合多階算術編碼也是一種有前景的壓縮方案。
前景與展望
BWT 是一種非常實用的可逆變換方法, 經BWT變換後的數據具有聚類效應, 利於壓縮。在分析研究了試驗結果之後, 發現把 BWT 與多階算術編碼、LZW 編碼結合起來的壓縮方案, 很適合於對大檔案的壓縮。在 BWT 中如何實現線性時間排序以及數據塊大小對壓縮編碼效率的影響是接下來非常有前景的算法研究問題。
