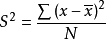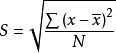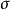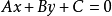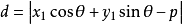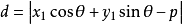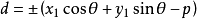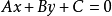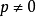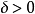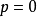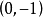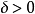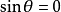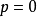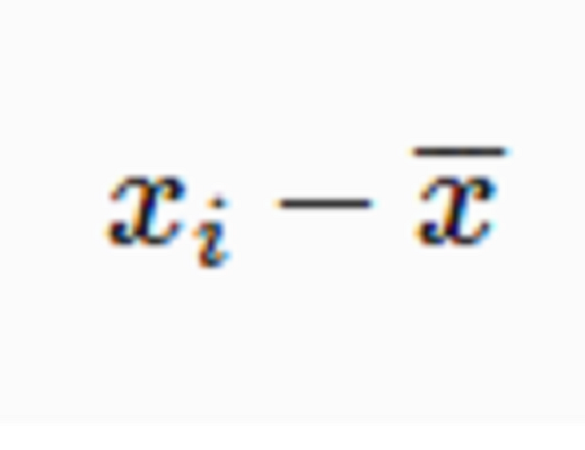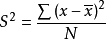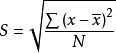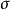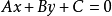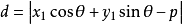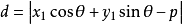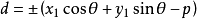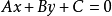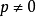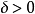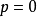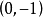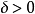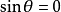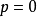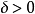基本介紹
- 中文名：離差
- 外文名：deviation
- 所屬學科：數學
- 相關概念：離散程度，標準差，平均數等
反映離散程度,基本介紹,全距,四分位區間距,平均差,方差與標準差,點於直線離差,
反映離散程度
基本介紹
離差即標誌變動度，又稱“偏差”，是觀測值或估計量的平均值與真實值之間的差，是反映數據分布離散程度的量度之一，或說是反映統計總體中各單位標誌值差別大小的程度或離差情況的指標，常寫作
，即參與計算平均數的變數值與平均數之差。離差的性質有二： (1)離差的代數和等於0；(2)參與計算平均數的各變數值與平均數之差的平均和，小於這些變數值與平均數之外的任何數之差的平均和。由於這兩種性質，使離差在描述統計中運用較廣。
在統計中用來測定標誌變動度的指標主要有：平均差、標準差。全距，四分位差，十分位差和離散係數等，離差是測定樣本代表性的重要指標，例如我們在選擇時，有兩組工人，每組都是5人，第一組每人日產分別為10，23，45，52，60，平均每人日產38件；第二組每人日產分別為35，39，42，39，38，平均每人日產也是38件，但我們可以看出，第二組的樣本較第一組樣本更加接近平均數，因此，第二組代表也較第一組強，從這裡可以看出，標誌變動度越小，樣本的代表性較強，反之，則樣本的代表性越強。
儘管集中量可以很好地描述一組數據的特徵，但僅用這些統計量還是不夠的。還需要考慮數據的分散情況。有時，兩組數據的平均數和中位數可能完全相同，但這兩組數據之間會存在著很大的區別。請看下面兩組數據：
A組：79 79 79 80 81 81 81
B組：50 60 70 80 90 100 100
這兩組數據的平均數和中位數均為80，但不能據此就簡單認為這兩組學生的水平是一樣的。A組數據與B組數據之間顯然是有區別的。首先，A組中的數據相對比較集中，每個數據的值與平均數80相差無幾；而B組中的數據相對分散一些，參差不齊，它反映了數據分布的另一個重要特徵——變異性(variability)。描述數據離散趨勢的統計量稱為離散量(measures of dispersion)，或稱差異量。
集中量描述了一組數據的典型情況，離散量則反映了數據的特殊情況。在研究一組數據的特徵時，不但要了解其典型情況，而且還要了解其特殊情況，前面的例子中A組數據和B組數據的集中量相同，但其離散量肯定是不同的，只有同時了解了這兩組數據的集中量和離散量，才能更為透徹地了解這兩組數據之間的差別。常用的表示數據離散趨勢的統計指標有全距、四分位區間距、平均差、方差和標準差。
全距
全距是說明數據離散程度的最簡單的統計量。把一組數據按從小到大的順序排列，用最高分減去最低分，所得的值就是全距，即最高分和最低分之問的距離。上面A組數據的全距為81-79=2；B組數據的全距為100-50=50。全距小，說明數據的分布相對集中；全距大，說明數據的分布較為分散。全距的優點是計算方法簡單，而且也容易理解。缺點是由於它只考慮到兩端的數值，沒有考慮中間數值的差異情況，描述數據時不太穩定。
四分位區間距
中位數可以用來表示一組數據分布的集中趨勢。中位數正好把一組數據一分為二。如果把中位數左側和右側的分布再各分成兩個部分，得到的是四個相等的分位。這組數據的第一個四分位(即25%的位置)的值正好處於數據分布的四分之一處，中位數正好是第二個四分位的值，第三個四分位的值剛好位於該組數據分布的四分之三處。把第三個四分位的值減去第一個四分位的值，所得到的值叫做四分位區間距(inter-quartile range，IQR)，統計學上也用這種方法來表示數據的離散情況。如上面A組數據的四分位區間距為81-79=2；B組數據的四分位區間距為100-60=40。除了四分位區間距，統計學上還有十分位區間距和百分位區間距，它們的區分方法相同，十分位則將數據由大到小或由小到大排序後，用9個點將全部數據分為十等份，與9個點位置上相對應的變數稱為十分位數(deciles)，分別記為D1,D2,...,D9，表示10%的數據落在D1下，20%的數據落在D2下……100%的數據落在D9下。百分位區間距與十分位區間距同例，只是將數據分成100等份，於99個分割點位置上相對應的變數稱為百分位數(Percentiles)，分別記為P1，P2，…，P99，表示1%的數據落在P1下……99%的數據落在P99下。
平均差
與全距相比，四分位區間距在表述數據的離散情況時稍微好一些，但由於它沒有把所有的數據都考慮在內，其穩定性會差一些。比如說，我們得到兩組數據，這兩組數據的值並不完全一樣，但最後得到的四分位區間距的值則可能完全一致，這便是用四分位區問距來表示數據分布的不足之處。理想的辦法是把全部數據都考慮在內來計算分布程度。理由很簡單：平均數代表一組數據的集中趨勢，我們把一組數據中的每個數據與平均數相比較就可以得知每個數據與平均數偏離的程度，或者說與平均數差異的情況。如果把這組數據中每個數據與平均數差異的情況相加起來，那么所有數據的差異情況便一目了然。把這個值除以數據的個數，所得的值叫做平均差。其計算公式為：
平均差=
其中，
=每個數據的值；
N=觀測的數據個數。
從上式可知，平均差是數據分布中所有原始數據與平均數距離的絕對值的平均。用絕對值是為了不出現負數。由於平均差是根據分布中每一個觀測值計算求得的，它較好地代表了數據分布的離散程度。然而，由於平均差的計算要求絕對值，不利於進一步的統計分析，故在統計實踐中平均差不常使用。
方差與標準差
根據上面的公式，如果不求每個原始數據與平均數之差的絕對平均值，而是求它們之間的平方，這樣就不會有負數出現了。然後再把每個原始數據與平均數之差的平方的值加起來，得到的是每個原始數據與平均數之差的平方和：
。用這個平方和再除以所觀測到的數據的個數，得到的值被稱作方差。用公式表示為：
。由於方差的值相對來說比較大，一般情況下人們使用標準差來代表數據的離散程度。標準差就是方差的平方根，其計算公式為：
。標準差與方差的概念易於理解，它們實際上都是一個差異量數：標準差的平方就是方差，或方差的平方根就等於標準差，二者都反映了一組數據圍繞平均數分布的情況。標準差的值越大，表明這組數據的離散程度也越大，即數據越參差不齊，分布範圍越廣；標準差的值越小，表明這組數據的離散程度越小，即數據越集中、整齊，分布範圍越小。當數據完全沒有差異時，所有數值都與平均數相等，這時標準差或方差等於零。
有一點需要說明：在上述公式中我們用N作為除數，所得結果並不是十分準確的。這是因為在一般情況下，總體參數是未知的，只能用樣本統計量作估計值，譬如用樣本標準差(S)作為總體標準差(
)的估計值。可以證明，在公式中用N作為除數時(尤其是當N很小時)，所得出的作為總體標準差估計值的樣本標準差是有偏差的，而N-1作除數時，所得標準差則是無偏差的。因此，比較穩妥的做法是用N-1作除數。當然，當N比較大時，用N或N-1作除數，所得結果差別不大。
點於直線離差
直角坐標平面上，
點到直線
的距離
根據這一公式，求一點到一條直線的距離，只要先把這條直線的方程化成法線式，然後把已知點的坐標代入方程的左邊，計算所得值的絕對值，就是所求的距離。
若將公式 ，寫成
，則其中的正負號應這樣確定：①當已知點和原點在直線的兩側時取正號；②當已知點和原點在直線的同側時取負號；③若直線過原點但不與Y軸重合，則已知點在直線上方時取正號，在直線下方時取負號；④若直線與Y軸重合，則已知點在直線右方時取正號，在直線左方時取負號。
離差δ的正負的判定法則是：①當
，或
時，若點 與原點在直線的同側，則
；異側，則
；②當
，或
(直線過原點)時，若點 與點
在直線同側，則 ；異側，則 ；③當
且 ，或
(直線為Y軸)時，若點 在直線右側，則 ;左側，則 。
離差不僅反映出點到直線的距離，而且顯示出點相對於直線的方位。
