基本介紹
四平方和定理
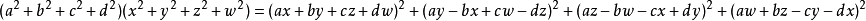
華林猜想
研究進展

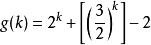

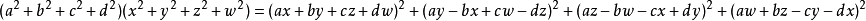

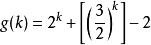
華林問題是數論中的問題之一。1770年,愛德華·華林猜想,對於每個非1的正整數k,皆存在正整數g(k),使得每個正整數都可以表示為至多g(k)個k次方數(即正整數的...
廣義除數問題(generalized divisor problem)是數論中的重要問題。數論是研究數的性質和規律的一門學科。是數學的一個重要分支。對於數學的許多分支學科(例如函式論、...
《數學的100個基本問題》是 2004年1月1日山西科學技術出版社出版的圖書,作者是靳平。...
愛德華·華林(Edward Waring,1736年-1798年8月15日),出生於英格蘭什羅普郡古希思,數學家。...
楊武之最好的工作是關於稜錐數的華林問題。稜錐數p(n)=1/6(n3-n)是三角形數f(n)=n/2(n十1)的推廣。1640年,費馬(Fermat)猜測每個正整數都是不超過3個...
李紅澤, 男,上海交通大學數學系教授、博士生導師。在科研方面一直從事解析數論的研究,主要致力於哥德巴赫問題,華林問題和Dirichilet L-函式零點分布等問題的研究,...
在研究哥德巴赫猜想和華林問題中,近代堆壘數論自20世紀20年代開始發展起來,主要的研究方法有圓法、指數和方法、篩法和密率。 堆壘數論中有以下幾個著名問題。...
祖沖之發現的圓周率的分數近似值π≈355/113,稱為密率,它是相對於約率π≈22/7而言的;還有一個含義是指數論中的一個重要概念,是與哥德巴赫猜想及華林問題有關...
加性數論,又稱堆壘數論,是數論的一個分支。它研究的主要問題是將整數表示成滿足特定條件的另一些整數的和,例如哥德巴赫猜想、華林問題、整數分拆問題、平方和問題...
用華氏定理基本上可以將依·維諾格拉朵夫關於華林問題的重要結果推廣至不定方程(1), 即假定(1)滿足必須滿足的條件,則當s>=s0 =O(Klog K)及N充分大時, (1...
余紅兵,男,1962年10月生,現在蘇州大學數學科學學院任教。主要從事解析數論及組合數論的研究。在整值多項式的華林問題、指數和及特徵和的估計、有限阿貝爾群的零和...
四平方和定理說明每個正整數均可表示為4個整數的平方和。它是費馬多邊形數定理和華林問題的特例。...
四平方和定理說明每個正整數均可表示為4個整數的平方和。它是費馬多邊形數定理和華林問題的特例。...
兩平方數之和(sum of two squares)與華林問題有關的一個數論問題。若對自然數n,存在整數x,y,使n=x2+y2,則稱n可表示為兩平方數之和。若在此基礎上,有...
