有向系統(directed system)是特殊的有向偏序集。若一個偏序集的任意兩個元素有上界，則稱此偏序集為有向偏序集。
基本介紹
- 中文名：有向系統
- 外文名：directed system
- 領域：數學
- 學科：集合論
- 性質：特殊的有向偏序集
- 集合：冪集
概念,偏序集,全序集,冪集,集合,
概念
有向系統(directed system)是特殊的有向偏序集。若一個偏序集的任意兩個元素有上界，則稱此偏序集為有向偏序集。設P(A)表示A的冪集，B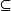
P(A)，並且B≠∅。若〈B，
〉是一個有向偏序集，則稱B是一個有向系統，其中〈B，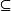
〉表示B關於集合包含關係構成的偏序集。
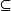
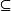
偏序集
偏序集是特定的集。它是一類主要的序關係集。具體地說，集合E連同其上的偏序R構成的關係集(E，R)，一般記為P=(E，≤)。所謂偏序(或序關係)是一類具有自反性、反對稱性和傳遞性的二元關係。例如，數之間的不大於關係，自然數之間的整除關係，集合之間的包容關係等。把集合E的基數稱為偏序集P的階。階為有限值的偏序集稱為有限偏序集。而在P上，對於任意元素x，y，區間[x，y]均為有限偏序集時，稱P為局部有限偏序集。這兩類偏序集是組合理論中的主要研究對象。偏序集上所有鏈的長度的最小上界，或上確界，稱為偏序集的長度，記為l(P)。偏序集中最大反鏈包含的元素數目，稱為偏序集的寬度，記w(p)。對於以下圖為哈塞圖的偏序集P，有l(P)=3，w(P)=2。偏序集的子關係集仍為偏序集，而且必有全序集作為其子關係集。
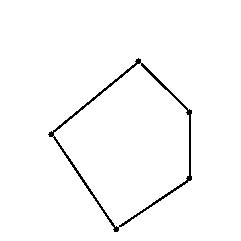圖1. 偏序集全序集
全序集亦稱線性序集。又稱鏈.一類重要的偏序集。若偏序集P適合公理P4：若對任意x，y∈P，x<y，y<x，x=y三式中有且僅有一式成立，則稱P為全序集。全序集中的關係≤稱為全序或線性序。若偏序集P的子集C作為子偏序集是全序集，則稱C是P中的鏈;若C是非序的，則稱C為P的反鏈。實數集及其任何子集在通常的≤關係下是全序集。
冪集
若A是一個集合，則以A的一切子集作為元素所組成的集合就叫做集合A的冪集。記作P(A)，即：P(A)={x|x⊆A}。
例如，設集合A={1，2}，則P(A)={Φ，{1}，{2}，{1，2}}。
由於集合A的任意兩個子集的並、交、差仍然是A的子集，因此A的冪集P(A)對於集合運算並、交、差是封閉的。
若A是由n個元素組成的集合，則它的冪集P(A)含有2個元素。
集合A的基數(參見“集合的基數”)小於它的冪集P(A)的基數。
空集Φ的冪集P(Φ)是非空集合，它有一個元素Φ。
集合
集合是現代數學的一個重要的基本概念。當我們把一組確定的事物作為整體來考察時，這一整體就叫做集合。
例如，(1)從1到10這10個自然數的全體；(2)小於100的所有質數的全體；(3)全體自然數；(4)一個班所有學生這一整體；(5)世界上所有國家組成的一個整體；等等，它們都是集合的例子。
上述例子可以看出，它們都是分別由不同的對象組成的一個整體，它們的特點是有確定的對象和具有一定的範圍。所以集合這個概念可以用以下的語言來描述：
集合是具有一定範圍的、確定的對象的全體。集合也簡稱為集。
在數學中，集合是一個不加定義的“原始概念”。這就是說，不能用比它更原始的概念去定義它。因此，集合在數學中被作為原始的最基本的概念來定義其它數學概念。集合是數學概念的出發點。
集合概念具有以下一些屬性：
(1)集合指的是一類事物的整體，而不是指其中的個別事物。
(2)集合中的任一對象具有確定性，即對於任何事物，可以通過某種法則確定其是否屬於某集合，或不屬於某集合，二者必居其一。(應指出，不具有這條屬性的，界限不清的集合是模糊集合。我們這裡所說的集合不是模糊集合，而是普通集合。)
(3)在一般情況下，約定一個集合中的各個對象是互不相同的。凡一個集合中所有相同的對象均應合併起來成為一個對象。例如，由1，1，2，2四個數組成的集合，應變成由1，2兩個數組成的集合。
(4)在一般情況下，集合只與組成它的成員有關，而與它的成員的順序無關。如由1，2，3，4組成的集合與由2，1，4，3組成的集合是同一個集合。
(5)一個集合不必由同一類事物作為它的對象。例如，由2， 3，a，b可以組成一個集合。
集合一般用大寫字母A，B，C，…表示。
