最臨近插值:使用情況,其他算法,解決方案,工作原理,線性插值,技巧,雙線性插值,獲

最臨近插值，通常被用於圖像縮放中，進行縮放圖像的方法叫做最臨近插值算法，這是一種最基本、最簡單的圖像縮放算法。效果並不好，放大後的圖像有很嚴重的馬賽克，縮小後的圖像有很嚴重的失真；效果不好的根源就是其簡單的最臨近插值方法引入了嚴重的圖像失真。

使用情況,其他算法,解決方案,工作原理,線性插值,技巧,雙線性插值,獲取對應值,注意,代碼,

使用情況

一般最臨近插值用於圖像縮放中

圖像的縮放很好理解,就是圖像的放大和縮小。傳統的繪畫工具中,有一種叫做“放大尺”的繪畫工具，畫家常用它來放大圖畫。當然，在計算機上，我們不再需要用放大尺去放大或縮小圖像了，把這個工作交給程式來完成就可以了。下面就來講講計算機怎么來放大縮小圖象；在本文中，我們所說的圖像都是指點陣圖，也就是用一個像素矩陣來描述圖像的方法，對於另一種圖像：用函式來描述圖像的矢量圖，不在本文討論之列。

越是簡單的模型越適合用來舉例子，我們就舉個簡單的圖像：3X3 的256級灰度圖，也就是高為3個像素，寬也是3個像素的圖像，每個像素的取值可以是 0－255，代表該像素的亮度，255代表最亮，也就是白色，0代表最暗，即黑色。假如圖像的像素矩陣如下圖所示（這個原始圖把它叫做源圖，Source）：

234 38 22

67 44 12

89 65 63

這個矩陣中，元素坐標(x,y)是這樣確定的，x從左到右，從0開始，y從上到下，也是從零開始，這是圖象處理中最常用的坐標系，就是這樣一個坐標：

---------------------->X

∨Y

如果想把這副圖放大為 4X4大小的圖像，那么該怎么做呢？那么第一步肯定想到的是先把4X4的矩陣先畫出來再說，好了矩陣畫出來了，如下所示，當然，矩陣的每個像素都是未知數，等待著我們去填充（這個將要被填充的圖的叫做目標圖,Destination）：

? ? ? ?

然後要往這個空的矩陣裡面填值了，要填的值從哪裡來來呢？是從源圖中來，好，先填寫目標圖最左上角的象素，坐標為（0，0），那么該坐標對應源圖中的坐標可以由如下公式得出：

srcX=dstX* (srcWidth/dstWidth) , srcY = dstY * (srcHeight/dstHeight)

好了，套用公式，就可以找到對應的原圖的坐標了(0*(3/4),0*(3/4))=>(0*0.75,0*0.75)=>(0,0),

找到了源圖的對應坐標,就可以把源圖中坐標為(0,0)處的234像素值填進去目標圖的(0,0)這個位置了。

接下來,如法炮製,尋找目標圖中坐標為(1,0)的象素對應源圖中的坐標,套用公式:

(1*0.75,0*0.75)=>(0.75,0)

結果發現,得到的坐標裡面竟然有小數,這可怎么辦?計算機里的圖像可是數字圖像,像素就是最小單位了,像素的坐標都是整數,從來沒有小數坐標。這時候採用的一種策略就是採用四捨五入的方法（也可以採用直接舍掉小數位的方法），把非整數坐標轉換成整數，好，那么按照四捨五入的方法就得到坐標（1，0），完整的運算過程就是這樣的：

(1*0.75,0*0.75)=>(0.75,0)=>(1,0)

那么就可以再填一個象素到目標矩陣中了，同樣是把源圖中坐標為(1,0)處的像素值38填入目標圖中的坐標。

依次填完每個像素，一幅放大後的圖像就誕生了，像素矩陣如下所示：

234 38 22 22

67 44 12 12

89 65 63 63

這种放大圖像的方法叫做最臨近插值算法，這是一種最基本、最簡單的圖像縮放算法，效果也是最不好的，放大後的圖像有很嚴重的馬賽克，縮小後的圖像有很嚴重的失真；效果不好的根源就是其簡單的最臨近插值方法引入了嚴重的圖像失真，比如，當由目標圖的坐標反推得到的源圖的的坐標是一個浮點數的時候，採用了四舍五入的方法，直接採用了和這個浮點數最接近的象素的值，這種方法是很不科學的，當推得坐標值為 0.75的時候，不應該就簡單的取為1，既然是0.75，比1要小0.25 ，比0要大0.75 ,那么目標象素值其實應該根據這個源圖中虛擬的點四周的四個真實的點來按照一定的規律計算出來的，這樣才能達到更好的縮放效果。雙線型內插值算法就是一種比較好的圖像縮放算法，它充分的利用了源圖中虛擬點四周的四個真實存在的像素值來共同決定目標圖中的一個像素值，因此縮放效果比簡單的最鄰近插值要好很多。

其他算法

雙線性內插值算法描述如下:

對於一個目的像素，設定坐標通過反向變換得到的浮點坐標為(i+u,j+v) (其中i、j均為浮點坐標的整數部分，u、v為浮點坐標的小數部分，是取值[0,1)區間的浮點數)，則這個像素得值 f(i+u,j+v) 可由原圖像中坐標為 (i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)所對應的周圍四個像素的值決定，即：

f(i+u,j+v) = (1-u)(1-v)f(i,j) + (1-u)vf(i,j+1) + u(1-v)f(i+1,j) + uvf(i+1,j+1) 公式1

其中f(i,j)表示源圖像(i,j)處的的像素值，以此類推。

比如，象剛才的例子，現在假如目標圖的象素坐標為（1，1），那么反推得到的對應於源圖的坐標是（0.75 , 0.75）, 這其實只是一個概念上的虛擬象素,實際在源圖中並不存在這樣一個象素,那么目標圖的象素（1，1）的取值不能夠由這個虛擬象素來決定，而只能由源圖的這四個象素共同決定：（0，0）（0，1）（1，0）（1，1），而由於（0.75,0.75）離（1，1）要更近一些，那么（1,1）所起的決定作用更大一些，這從公式1中的係數uv=0.75×0.75就可以體現出來，而（0.75,0.75）離（0，0）最遠，所以（0，0）所起的決定作用就要小一些，公式中係數為(1-u)(1-v)=0.25×0.25也體現出了這一特點；

後記：近日在論壇上看到有人提問，說寫的圖像縮放算法放大圖片的時候出現了空缺。分析了一下代碼，發現是犯了這樣的錯誤：縮放圖片的時候，遍歷源圖的像素，然後推出目標圖中的對應坐標，進行逐點的像素拷貝，這樣當然放大圖片的時候會出現空缺。縮小圖片的時候結果是對的，但是會出現多餘的計算量。

圖像縮放算法一定要反推：遍歷目標圖的像素，反推得到源圖中的對應坐標，然後進行像素拷貝。這樣才保證了放大圖片沒有空缺，縮小圖片也不會引入冗餘計算。

以上內容沒有設計到雙線性內插值算法計算公式的具體原理，下面簡單分析下：

當你製作一個使用地形的遊戲時，你需要知道地形確定點的精確高度。例如，在地形上移動一個模型時(見教程4-17)，當檢測到游標和地形之間的碰撞時（下一個教程），或防止相機與地形碰撞時（見教程2-6）。

因為在前一個教程中你定義了地形每個頂點的3D位置，所以獲取這些點的高度很簡單。對位於這些頂點間的位置而言，你需要使用一種插值方法獲取這個位置的精確高度。

解決方案

如果你想知道高度的點與地形的一個頂點發生碰撞，那么你已經知道了地形上該點的精確高度。如果這個點並沒有與頂點發生碰撞，那么說明這個點在地形的一個三角形上。因為三角形是一個平面，所以你可以通過在三角形三個頂點間進行插值獲取任何點的精確高度。

工作原理

首先從X和Z坐標開始，你想知道該點的對應Y坐標，這可以通過對三角形三個頂點的高度進行插值獲取。

這意味著你首先要找到點究竟在哪個三角形中，這並不容易。但首先我想介紹插值。

線性插值

如果你只處理分離的數據、想知道分離點之間的某些值，需要用到某種類型的插值。這種情況如圖5-17坐標所示。對某些分離的(整數) X值，你知道Y值。當X=2，你知道Y=10，X=3時Y=30。但你不知道X=2.7時的Y值。

圖5-17 線性插值：簡單常規的例子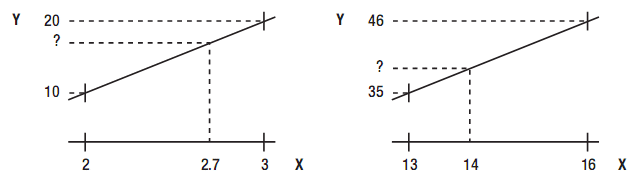

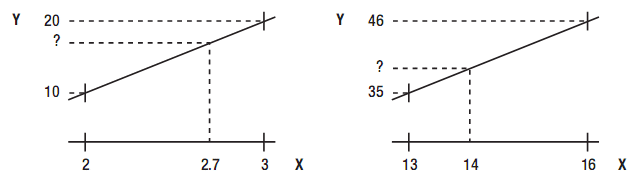
使用線性插值，你通過連線兩點的線段找到X=2.7對應的Y值，如圖5-17所示。使用線性插值，通過連線兩點的線段找到X=2.7對應的Y值。線性插值總是將X表達成0和1之間，0對應X的最小值（你知道對應的Y值，本例中為2），1對應X的最大值（本例中為3）。本例中你想找到X=2.7時的Y值，結果是0.7，意思是“2和3至之間的70%。”

在圖5-17的左圖中，0%對應Y值10，100%對應Y值20，所以70%對應Y=17。這很容易看出，但右圖的情況如何？14對應0.33，因為它是13和16之間的33%。但35和46之間的33%是多少？顯然，你希望有代碼可以為你計算結果。

首先要有代碼找到0和1對應的值。從X值開始，首先減去最小的X值，這樣最小值變為0。然後，將最大值縮放為1，你可以通過將它除以最大值和最小值之差實現。

下面是圖5-17左圖的做法： 2.7→(2.7－min)/(max－min)=(2.7－2)/(3－2)=0.7

然後，進行逆運算獲取對應的Y值：首先縮放這個值(通過乘以最大值和最小值的差值)，並加到最小的Y值上：

0.7* (maxY－min Y)+minY=0.7*(20－10)+10=0.7*10+10=17

這裡你採取圖5-17左圖簡單例子的規則，但你可以使用這個方法計算任何線性插值。看一下圖5-17右圖更難的例子，在這種情況中，你知道X=13對應Y=35，X=16對應Y=46，但你想知道X=14對應的Y值。所以，首先獲取0和1之間對應的值：

14→(14－minX)/(maxX－minX) =(14－13)/(16－13)=0.33

知道了對應值，就做好了獲取對應Y值的準備：

0.33* (maxY－minY)+minY=0.33*(46－35)+35=0.33*11+35=3.67+35=38.67

最後，需要進行浮點計算。圖5-17的右圖中找到X=14對應Y=38.67。事實上，幾乎所有插值計算都返回一個浮點數。

技巧

XNA提供了一個功能可以為你計算Vector2, Vector3或Vector4的插值。例如，如果你想獲取哪個Vector2位於(5,8)和(2,9)之間的70%，你可以使用Vector2. Lerp(new Vector2(5,8), new Vector2(2,9), 0.7f)。

雙線性插值

在地形的例子中，對所有(X,Z)值，你已經定義了一個頂點並知道了它的精確高度。對所有在這些獨立頂點之間的(X,Z)值，你不知道精確的Y值，所以需要進行插值。這次你需要獲取0和1之間的值，包含X和Z。

有了這些值，就可以分兩步計算出精確的Y值。

獲取對應值

給定任意(X,Z)坐標，你需要找到地形上的精確Y高度。首先使用前面的公式找到對應的X和Z值，但這次因為在3為空間中，你需要用兩次：

int xLower = (int)xCoord; int xHigher = xLower + 1; float xRelative = (xCoord - xLower) / ((float)xHigher - (float)xLower); int zLower = (int)zCoord; int zHigher = zLower + 1; float zRelative = (zCoord - zLower) / ((float)zHigher- (float)zLower); 在地形中每個X和Z的整數值你定義了一個頂點，所以你知道精確的Y值。所以對每個X的浮點數，你要將它們轉換為整數獲取最小的X值(例如，2.7變為2)。將這個值加1獲取最大X值(2.7對應3作為最大值)。知道了邊界，很容易使用前面的公式找到對應值。Z值的求法類似。

獲取minY和maxY的值

知道了0和1之間的對應值，下一步是找到精確Y值。但是，首先需要知道minY和maxY值。這些值表示頂點中的高度。你需要知道點在哪個三角形中才能知道使用哪個頂點的高度作為Y值。

你知道點P的X和Z坐標，所以你知道點周圍的四個頂點，很容易獲取它們的Y值：

float heightLxLz = heightData[xLower, zLower]; float heightLxHz = heightData[xLower, zHigher]; float heightHxLz = heightData[xHigher, zLower]; float heightHxHz = heightData[xHigher, zHigher]; LxHz表示“低X坐標，高Z坐標” 決定(X,Z)。

點在哪個三角形中用來繪製地形的兩個三角形。有兩個方式可以定義這兩個三角形，如圖5－18所示。繪製三角形的方式影響到P點的高度，如圖所示。

圖5-18 從四個頂點繪製兩個三角形的兩種方法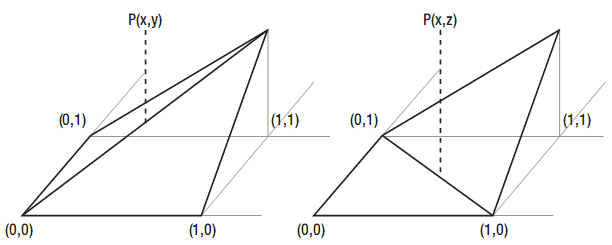

雖然四個頂點有相同的坐標，但兩種情況中的點的高度並不相同，圖中你可以可出明顯的區別。

基於我即將討論的理由，更好的方式是圖5－18的右圖。

使用這個旋轉方式，很容易確定點在哪個三角形上方。兩個三角形之間的邊界由對角線給出。在右圖中，如果xRelative + zRelative 為1的話，這條線對應具有X和Z坐標的點。

例如，如果這個點在四個點中央，如圖5－18所示，xRelative和zRelative都是0.5f，所以和為1，說明在對角線上。如果這個點偏向左邊一點，xRelative會小一些，和會小於1，對Z坐標也是類似的情況。所以如果和小於1，(X,Z)坐標位於左下角的三角形內；否則，該點在右上角的三角形內：

bool pointAboveLowerTriangle = (xRelative + zRelative < 1);

注意

圖5－16中定義的所有三角形都是以圖5－18右圖中的形式繪製的。

獲取精確高度

知道了對應高度，四個周圍頂點的高度和點位於哪個三角形中，你就可以計算精確高度了。

如果點在左下方的三角形中，這時pointAboveLowerTriangle為true，下面是使用雙線性插值獲取三角形任意點高度的代碼：

finalHeight = heightLxLz; finalHeight += zRelative * (heightLxHz - heightLxLz); finalHeight += xRelative * (heightHxLz - heightLxLz); 根據前面解釋的單插值的方法，從lowestX的Y值開始。因為這是“雙”插值，你要從lowestXlowestZ的Y值開始。

在單插值中，你maxY之間添加高度差，並乘以對應的X值。在雙插值中，你乘的是 zRelative和xRelative。

換句話說，從左下頂點的高度開始，對這個高度，你添加了這個頂點和有著更高Z坐標的頂點間的高度差，並乘以距離第二個頂點的Z坐標的接近程度。最後一行代碼類似：對這個高度，你添加了左下頂點和右下頂點的高度差，乘以距離右下頂點的X坐標的接近程度。

如果該點在右上三角形的內部，這時pointAboveLowerTriangle為false，情況有所不同，你需要以下代碼：

finalHeight = heightHxHz; finalHeight += (1.0f - zDifference) *(heightHxLz - heightHxHz); finalHeight += (1.0f - xDifference) * (heightLxHz - heightHxHz); 從高度開始，從右上頂點開始，遵循同樣的步驟：添加高度差，乘以對應距離。

代碼

這個方法包含前面解釋的所有代碼。基於任意(X,Z)坐標，無論是整數還是浮點數，這個方法返回該點的精確高度。首先檢查該點是否在地形上。如果不是，返回默認的高度10。

public float GetExactHeightAt(float xCoord, float zCoord) { bool invalid = xCoord < 0; invalid |= zCoord < 0; invalid |= xCoord > heightData.GetLength(0) - 1; invalid |= zCoord > heightData.GetLength(1) - 1; if (invalid) return 10; int xLower = (int)xCoord; int xHigher = xLower + 1; float xRelative = (xCoord - xLower) / ((float)xHigher - (float)xLower); int zLower = (int)zCoord; int zHigher = zLower + 1; float zRelative = (zCoord - zLower) / ((float)zHigher - (float)zLower); float heightLxLz = heightData[xLower, zLower]; float heightLxHz = heightData[xLower, zHigher]; float heightHxLz = heightData[xHigher, zLower]; float heightHxHz = heightData[xHigher, zHigher]; bool pointAboveLowerTriangle = (xRelative + zRelative < 1); float finalHeight; if (pointAboveLowerTriangle ) { finalHeight = heightLxLz; finalHeight += zRelative * (heightLxHz - heightLxLz); finalHeight += xRelative * (heightHxLz - heightLxLz); } else { finalHeight = heightHxHz; finalHeight += (1.0f - zRelative) * (heightHxLz - heightHxHz); finalHeight += (1.0f - xRelative) * (heightLxHz - heightHxHz); } return finalHeight; } 原理 線性插值並不難理解。以圖像處理領域為例，我們的理想圖像是均勻的分布在二維平面直角坐標系中的，任意給出一對坐標，就應該能夠得到一個對應的顏色值，然而現實是殘酷的，我們只能夠用離散的點陣信息來近似表現圖像。 現在假設給定一對坐標（2.2, 4.0），想要得到這個坐標對應的顏色，那么比較簡單的方法是用四捨五入方法來得到距離該點最近的像素，即像素 (2, 4)的值來代替，這顯然並不十分的精確，如果用這個方法進行圖像放大，那么在比例較大的情況下就會出現明顯的“馬賽克”現象。 對於上面的例子，更好的辦法是把像素(2, 4)和像素(3, 4)的值按照一定的比例混合。比例如何選取呢？很簡單，離哪個像素近，哪個像素的比例就大些。那么（簡單起見，後面均假設是灰度圖），若設像素 (2, 4)的值是V_24，像素(3, 4)的值是V_34，就可以得到： 坐標(2.2, 4.0)的顏色值 V(2.2, 4.0) = V_24*(1-0.2)+V_34*0.2 好，現在你已經懂得什麼叫線性插值了! 二次線性插值也就不難理解了。這次我們給的坐標不再是那么體貼了——求坐標(2.2, 4.6)的顏色值。那么可以想到：可以先分別求出坐標(2.2, 4.0)和坐標(2.2, 5.0)的顏色值，然後用一次縱向的線型插值，就得到了： 坐標(2.2, 4.0)的顏色值 V(2.2, 4.0) = V_24*(1-0.2)+V_34*0.2 坐標(2.2, 5.0)的顏色值 V(2.2, 5.0) = V_25*(1-0.2)+V_35*0.2 坐標(2.2, 4.6)的顏色值 = V(2.2, 4.0)*(1-0.6)+V(2.2, 5.0)*0.6 到這裡，實際上我們已經得到了二次線性插值的計算公式，表述方便起見下面用符號來表示。 設坐標(x, y)的相鄰四個像素值分別為p00, p01, p10, p11, 水平方向的比例係數為h0, h1, 垂直方向的比例係數v0, v1（其中h0+h1=1, v0+v1=1），那么用bilinear interpolation得到： v(x, y) = (p00*h0+p01*h1)*v0 + (p10*h0+p11*h1)*v1 ................(1.1) 有了這個公式，已經可以編寫出算法了，但是這個公式里有六次浮點乘法，如果是真彩圖的話，則對每一像素都要有18次浮點乘法！這還不算生成浮點坐標值的時間（比如在旋轉算法當中，每得到一對浮點坐標還要有若干次浮點運算）。 最佳化 學過一些線性代數知識的朋友可能已經注意到，公式(1.1)其實可以寫成矩陣連乘的形式： |p00 p01| |h0| v(x, y) = |v0 v1|*| |*| | ................................(1.2) |p10 p11| |h1| 那么我們就可以利用矩陣相乘的運算法則來最佳化算法。首先，這裡的運算瓶頸是v0, v1, h0, h1這四個浮點值帶來的，而實際上我們需要這么高的精度嗎？p00, p01, p10, p11以及我們的運算結果都是整數（對於我們的情況，是0-255之間的整數）。也就是說，其實把我們的結果最後賦值給v(x, y)時，小數部分已經被截掉了，我們根本用不到那么高的精度！那么我們可以嘗試用整數乘法代替浮點乘法。 比如，令V0 = (int)(v0*65536.0+0.5)，V1 = 65536-V0，H0 = (int)(h0*65536.0+0.5), H1 = 65536-H0，那么有： |p00 p01| |H0| v(x, y)*65536*65536 = |V0 V1|*| |*| | ....................(1.3) |p10 p11| |H1| 計算出(1.3)式右邊的值，左邊就可以用右移來代替除法計算出v(x, y)的值。當然實際實現算法的時候，這個公式是一定會溢出的，因為有符號整數的最大值不過是+(32768*65536-1)，所以可以在運算中間過程中就進行移位運算。 當然，最佳化不能只局限於這個函式，否則是沒有意義的，在設計整個算法的時候（即需要用到bilinear interploation的某個圖像處理算法），就應該避免使用浮點，保證V0, V1, H0, H1是整形值。在WannaPlayDIB庫中，DIB_RotateFast就是個很好的例子，在循環中央的ox, oy如果不進行右移，就可以通過截取低16位值的方法來得到上面對應的H1和V1，而H0 = 65536-H1, V0 = 65536-V1。因此很容易就能寫出DIB_RotateFast的二次插值版本。 維基百科，自由的百科全書 雙線性插值，又稱為雙線性內插。在數學上，雙線性插值是有兩個變數的插值函式的線性插值擴展，其核心思想是在兩個方向分別進行一次線性插值。 紅色的數據點與待插值得到的綠色點 假如我們想得到未知函式 f 在點 P = (x , y ) 的值，假設我們已知函式 f 在 Q 11 = (x 1 , y 1 )、Q 12 = (x 1 , y 2 ), Q 21 = (x 2 , y 1 ) 以及 Q 22 = (x 2 , y 2 ) 四個點的值。首先在 x 方向進行線性插值，得到 然後在 y 方向進行線性插值，得到 這樣就得到所要的結果 f (x , y )， 如果選擇一個坐標系統使得 f 的四個已知點坐標分別為 (0, 0)、(0, 1)、(1, 0) 和 (1, 1)，那么插值公式就可以化簡為 或者用矩陣運算表示為 與這種插值方法名稱不同的是，這種插值方法並不是線性的，它的形式是 它是兩個線性函式的乘積。另外，插值也可以表示為 在這兩種情況下，常數的數目]都對應於給定的 f 的數據點數目。線性插值的結果與插值的順序無關。首先進行 y 方向的插值，然後進行 x 方向的插值，所得到的結果是一樣的。雙線性插值的一個顯然的三維空間延伸是三線性插值 /09/20/4573771.aspx</a>

最臨近插值