基本介紹
- 中文名:數論函式
- 外文名:number-theoretic function
- 別稱:算術函式
- 對象:正整數集
簡介

內容

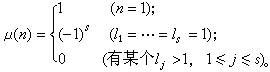 函式
函式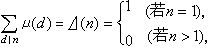 數論函式
數論函式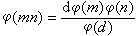 圖3.
圖3. 圖4.
圖4.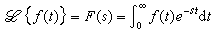 圖5.
圖5.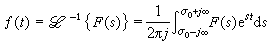 圖6.
圖6.狄利克雷卷積
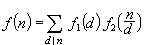 圖7.
圖7.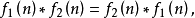

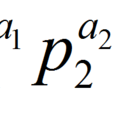


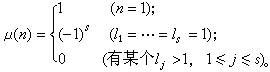 函式
函式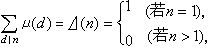 數論函式
數論函式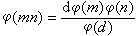 圖3.
圖3. 圖4.
圖4.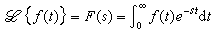 圖5.
圖5.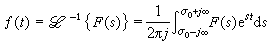 圖6.
圖6.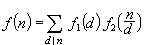 圖7.
圖7.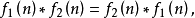

在數論上,算術函式(或稱數論函式)指定義域為正整數、陪域為複數的函式,每個算術函式都可視為複數的序列。最重要的算術函式是積性及加性函式。算術函式的最重要...
《數論算法(研究生)》是2014年西安電子科技大學出版社出版的圖書,作者是姜建國、臧明相。...
快速數論函式庫是一個的高度最佳化的C語言數論函式庫。主要功能包括整數、有理數和有限域上的多項式算術和二次篩法。...
切比雪夫函式(Chebyshev function)重要的數論函式之一。它是切比雪夫(Чебышев,П.Л.)為了證明素數定理而給出的。使函式Ψ(x)與對數函式建立了簡單的...
《數論講義》是2001年高等教育出版社出版的圖書。本書在介紹熟知的經典結果時,注意介紹新的證明方法和近代進展,並儘可能介紹它們的套用。...
《數論函式和數列的性質研究》是2011年12月23日科學出版社出版的圖書。該書可供高等院校數學系、數論愛好者學習,也可供數論和密碼學相關專業人員參考。...
杜德利所著的《基礎數論》對初等數論的大多數論題進行了介紹。推導了整數和同餘式的基本性質,給出了費馬定理和威爾遜定理的證明,介紹了幾個數論函式以及丟番圖...
默比烏斯函式,也稱為莫比烏斯函式、繆比烏斯函式,數論函式,由德國數學家和天文學家默比烏斯(August Ferdinand Möbius ,1790–1868)提出。梅滕斯(Mertens)首先...
界函式(bounding function)一種特殊函式。是時間或空間複雜性的限定函式。...... [1] 設M為一個算法,中為其一個複雜性測度.f為一元數論函式,若對任何字W,都...
初等數論是研究數的規律,特別是整數性質的數學分支。它是數論的一個最古老的分支。它以算術方法為主要研究方法,主要內容有整數的整除理論、同餘理論、連分數理論和...
《數論、群論、有限域》是2013年清華大學出版社出版的圖書,作者是周煒。...... 全書分為11章: 集合與函式,整除性理論,數論函式,不定方程,同餘式,二次剩餘,原根...
1、Excel中的N函式2、N函式(N-function)一種數論函式...... 1、Excel中的N函式 2、N函式(N-function)一種數論函式 一、Excel中的N函式N(value)...
剩餘函式(residual function)二元數論函式...... 剩餘函式(residual function)二元數論函式.對任何自然數二,刃y}o>,以y除二後所得之剩餘記為rs(.x,y),稱rs為...
黎曼ζ函式主要和“最純”的數學領域數論相關,它也出現在套用統計學和齊夫-曼德爾布羅特定律(Zipf-Mandelbrot Law))、物理,以及調音的數學理論中。...
《數論與有限域》是2010年機械工業出版社出版的圖書,作者是董麗華。...... 數論函式、二次剩餘以及原根與指數等內容;隨後兩章重點論述了近世代數中群、環、域的...
