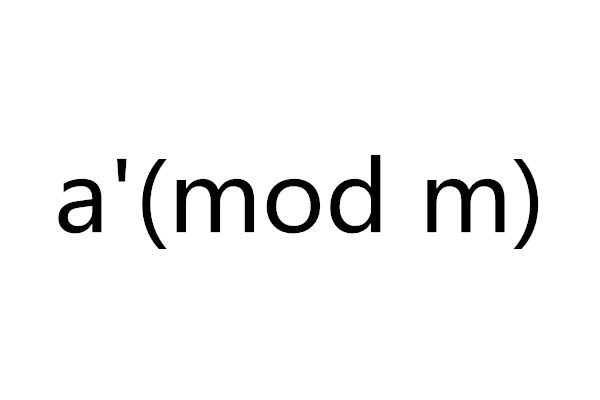數論倒數(number-theoretic reciprocal)亦稱算術倒數，是與同餘有關的一個基本概念。設m為模，a為任意整數，且(a，m)=1。若有整數a′能滿足同餘式a′a≡1(mod m)，則稱a′是a(mod m)的數論倒數，或逆元。例如，設整數a=2，m=3，且(2，3)=1，當a′=2時，有a′a≡2·2≡4≡1(mod 3)，則a′=2就是整數2(mod 3)的數論倒數。
基本介紹
- 中文名：數論倒數
- 外文名：number-theoretic reciprocal
- 所屬學科：數學
- 所屬問題：初等數論(同餘式)
- 簡介：與同餘有關的一個基本概念
- 相關定理：中國剩餘定理（孫子定理）
- 別稱：算術倒數
基本介紹,相關結論及介紹,孫子定理(中國剩餘定理),
基本介紹
設m∈N+，a∈Z，且(a，m)= 1，則稱滿足ax≡1(mod m)的整數x為a對模m的數論倒數，記為a-1(mod m)或a-1或a′(mod m)或a′。
①a-1定存在。
②a-1不唯一。
③(a-1，m)=1。
④(a-1)-1≡a( mod m)，(數論倒數是相互的)(均可由裴蜀定理得證)。
相關結論及介紹
⑴整數a存在數論倒數a′(mod m)的充分必要條件是(a，m)=1。
⑵數論倒數常用於求解同餘式組，例如，使用孫子定理求解同餘式組x≡b1(mod m1)，x≡b2(mod m2)，…，x≡bk(mod mk)時，此同餘式組的正整數解為
x≡b1M1′M1+b2M2′M2+…+bkMk′Mk(mod M)，
這裡Mi′就是滿足同餘式Mi′Mi≡1(mod mi)(i=1，2，…，k)關於Mi(mod mi)的數論倒數。式中M=m1m2…mk=m1M1=m2M2=…=mkMk，Mi=M/mi，且(Mi，mi)=1。
⑶設p為奇質數，對1<a<p-1在模p的意義下有
①1-1=1，(p-1)-1=p-1。
②1<a-1<p-1。
③若1<a<b<p-1，則a-1
b-1(mod p)，因而2，3，...，p-2中的數，可按數論倒數兩兩配對。
事實上，若a-1=b-1(mod p)，則1≡ab-1(mod p)，進而b≡a(mod p)，與條件矛盾。
孫子定理(中國剩餘定理)
在中國古代數學著作《孫子算經》中，有一道題目叫做“物不知數”：
有物不知其數，三三數之剩二，五五數之剩三，七七數之剩二。問物幾何?
亦即，求正整數解x滿足:
x= 2mod3
= 3mod5
= 2mod7
在1247年，中國數學家秦九韶做出了完整的解答，口訣如下：
三人同行七十希，五樹梅花廿一支，七子團圓正半月，除百零五便得知。
這個解法實際上是，首先利用秦九韶發明的“大衍求一術”求出5和7的最低公倍數35的倍數中除以3餘數為1的最小一個數70 (這個數稱為35相對於3的數論倒數)，3和7的最低公倍數21相對於5的數論倒數21，3和5的最低公倍數15相對於7的數論倒數15。然後計算
70x2+21x3+15x2= 233
233便是可能的解之一。它加減3、5、7的最低公倍數105的若干倍仍然是解，因此最小的解為233除以105的餘數23。以上解法若推廣到一般情況，便得到了中國剩餘定理（孫子定理）。
中國剩餘定理(Chinese Remainder Theorem，CRT)：
設
為兩兩互質的正整數，則對任意的整數
，存在整數x，使得x≡ci(mod mi)(1≤i≤k)同時成立。並且在模
的意義下，上述同餘方程組的解是唯一的， 可表示為x≡x0(mod m1m2...mk)，其中x0可以
這樣確定：令:
是
關於模
的數論倒數。則
。
