正多邊形內角和
已知
已知正多邊形內角度數則其邊數為:360°÷(180°-內角度數)
推論
任意正多邊形的外角和=360°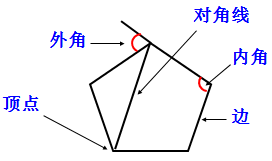
正多邊形任意兩條相鄰邊連線所構成的三角形是等腰三角形
多邊形的內角和
定義
〔n-2〕×180°(n為邊數)
多邊形內角和定理證明
證法一:在n邊形內任取一點O,連結O與各個頂點,把n邊形分成n個三角形.
因為這n個三角形的內角的和等於n·180°,以O為公共頂點的n個角的和是360°
所以n邊形的內角和是n·180°-2×180°=(n-2)·180°.(n為邊數)
即n邊形的內角和等於(n-2)×180°.(n為邊數)
證法二:連結多邊形的任一頂點A1與其不相鄰的各個頂點的線段,把n邊形分成(n-2)個三角形.
因為這(n-2)個三角形的內角和都等於(n-2)·180°(n為邊數)
所以n邊形的內角和是(n-2)×180°.
證法三:在n邊形的任意一邊上任取一點P,連結P點與其不相鄰的其它各頂點的線段可以把n邊形分成(n-1)個三角形,
這(n-1)個三角形的內角和等於(n-1)·180°(n為邊數)
以P為公共頂點的(n-1)個角的和是180°
所以n邊形的內角和是(n-1)·180°-180°=(n-2)·180°.(n為邊數)
重點:多邊形內角和定理及推論的套用。
難點:多邊形內角和定理的推導及運用方程的思想來解決多邊形內、外角的計算。
教學
1.複習四邊形、凸多邊形及有關概念。
⑴舉出生活中多邊形的實例;
⑵類比定義多邊形式、凸多邊形的概念,並指出如果
沒有特別說明,多邊形一般指凸多邊形;
⑵ 將四邊形的有關概念逐項擴展到多邊形情況,如頂
點、邊、內角、對角線表示方法等; 圖 4-10
⑷簡單練習,鞏固多邊形的表示方法及有關元素的辨認。
探索推導
1.提出問題。
由三角形內角和為180°,四邊形內角和為360° ,猜想多邊形的內角和度數與邊數有關。具體是什麼關係?
2.啟發學生猜想證明的思路。
⑴複習四邊形內角和定理的證明過程,強調把四邊形分割成三角形,從而“把四邊形內角和轉化為三角形內角和來研究”這種化歸的思想。
⑵引導學生類比聯想,用化歸的思想和從特殊到一般的方法研究五邊形、六邊形、七邊形……的情況。
①教師應幫助學生分析出解決問題的關鍵是多邊形分割轉化成有公共頂點的三角形的方法,以及割成三角形的個數與多邊數的關係;
②引導學生認識分割方法的多樣性(見設計說明),選擇其中較為簡單並引導大部分學生認識過程的分割方法,推導五邊形、六邊形……的情況,歸納出n邊形內角和的結論。
3.得到定理:n邊形的內角和等於(n-2)·180°。
說明:⑴多邊形的內角和僅與邊數有關,與多邊形的大小、形狀無關;
⑵強調凸多邊形的內角a的範圍:0°<α<180°。
練習
例1⑴22邊形的內角和是多少度?若它的每一個內角都相等,那么它的
每個外角度數是多少?
⑴ 幾邊形的內角和是八邊形內角和的2倍?
⑷已知一個多邊形,它的內角和等於外角和的2倍,求邊數。
分析:
①引導學生利用方程的思想,根據多邊形的內角和、外角和的性質及題目中提供的等量關係得出關於未知數的方程去求解;
②對於利用多邊形內角和公式反求邊數的題目,需注意:只有求出的邊數n是大於2的正整數時,問題才有解;
③靈活運用“多邊形的外角和與邊數無關的性質”簡化計算。
例2 ⑴已知多邊形的每個內角都是135°,求這個多邊形的邊數;
⑵每個外角都相等的多邊形,如果它的一個內角等於一個外角的9倍,求這個多邊形的邊數。
分析:
①每個內角或外角都相等的多邊形,它的每個內角為(n-2)·180°/n,從而利用360°/n,利用這兩點就可以列出關於邊數n的方程,其中第二種方法較為簡單。
②對於第⑴題,可將“每個角都是135°”轉達化為“每個外角都為45°”,從而利用360°/n=45°,得出n的值為8。
③若設邊數為n,則方程為(n-2)·180°/n=9×360°/n得出n=20。
(選用)例3 ⑴某多邊形除一個內角a外,其餘內角的和是2 750°。求這個多邊形的邊數。
⑵已知n邊形恰有四個內角是鈍角。這種多邊形共有多少個?其中邊數最少的是幾邊形?邊數最多的是幾邊形?
分析:利用多邊形每個內角a的範圍,0°<α<180°,以及題目所提供的角度關係列不等式解決問題。
解:⑴由題意得(n-2)·180°=α+2 750°,∴α=(n-2)·180°-2 750°。
又∵0°<α<180°,∴0°<;(n-2)·180°-2 750°<180°,
∴17 5/18<n<18 5/18。
因此這個多邊形為18邊形。
⑵設四個鈍角分別為α,β,γ,δ。則
∵360°<α+β+γ+δ<720°。
而另外n-4個內角都是直角或銳角,
∴(n-4)×0°<;其餘(n-4)個內角的和≤(n-4)×90°,
∴360°<(n-2)·180°<720°+(n-4)×90°,
即360°<(n-2)·180°<720°+(n-4)×90°,∴4<n<8。
∵4<n<8的整數n有5,6,7三個,
∴這樣的多邊形共有三個,其邊數最小的是五邊形,邊數最多的七邊形。
補充練習:
1.幾邊形的內角和與外角和之比是7∶2?(答:9)
2.已知一個多邊形的每個內角都是鈍角,這樣的多邊形有多少個?每個內角都是銳角的多邊形有多少個?是幾邊形?每個內角都是直角的多邊形有幾個?是幾邊形?(答:無數個;一個,三角形;一個,四邊形)
3.多邊形最多有幾個外角是鈍角?最多有幾個內角是銳角?(答:3個;3個)