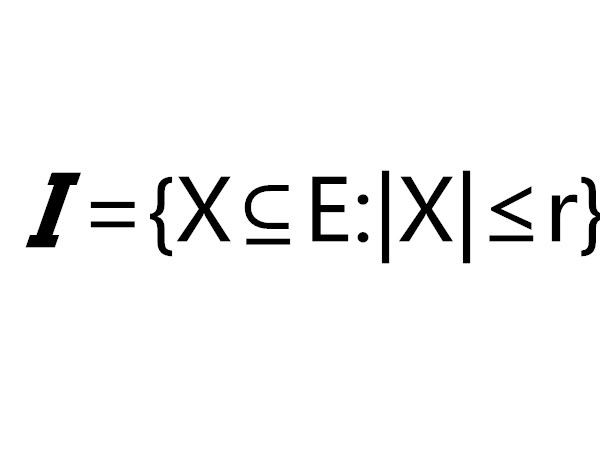均勻擬陣(uniform matroid)是一種特殊的擬陣,設n≥r≥0是兩個整數,E是一個含有n個元素的集合。如果I={X⊆E:|X|≤r},則稱(E,I)是一個均勻擬陣, 記為Ur,n。
基本介紹
- 中文名:均勻擬陣
- 外文名:uniform matroid
- 所屬學科:數學
- 所屬問題:組合學(組合序)
- 簡介:一種特殊的擬陣
基本介紹,廣義均勻擬陣,
基本介紹
均勻擬陣是只以有限集E的子集I中包含元素的數目多少決定其獨立性的擬陣Uk,n,其中n=|E|,E的子集B為擬陣的基,若且唯若B由k個元素組成。類似地,C為擬陣的圈,若且唯若C為k+1個元素組成。H為擬陣的超平面,若且唯若H由k-1個元素組成。例如,U2,3中的E視為歐氏空間裡一條直線上的3點,每一個單點構成U2,3的超平面,每兩點構成該擬陣的一個基,而全部三個點是它的惟一的圈。
廣義均勻擬陣
一個擬陣(matroid)M是一個有序對(E,J),其中E且是一個有限集合,J⊆2E是E中子集的集合,它們滿足以下的公理:
(I1)∅∈I。
(I2)若I∈J,及I'⊆I,則I'∈J。
(I3)若I1,I2∈J且|I1|<|I2|,則存在e∈I2-I1使得I1∪e∈J。
E上的擬陣獨立集系的全體記為 (E)。
(E)。

定義 設n≥r≥0為兩個整數,E是一個n元集,令
J={X⊆E:|X|≤r} ,
則(E,J) 是一個擬陣,這樣的擬陣稱為均勻擬陣。
定理1 設E 是一個有限集,B⊆E,m≤|B|,則令J( m,B,E) = { A∈2E||A∩B|≤m}∈ (E) ,稱J(m,B,E)是E上的關於集合B的m擬陣獨立集系( 簡稱廣義均勻擬陣獨立集系) ,且稱( E,J(m,B,E) ) 為關於集合B的帶獨立集系的m擬陣( 簡稱廣義均勻擬陣) ,E 上的廣義均勻擬陣的全體記為
(E) ,稱J(m,B,E)是E上的關於集合B的m擬陣獨立集系( 簡稱廣義均勻擬陣獨立集系) ,且稱( E,J(m,B,E) ) 為關於集合B的帶獨立集系的m擬陣( 簡稱廣義均勻擬陣) ,E 上的廣義均勻擬陣的全體記為 。
。


證明 很顯然J(m,B,E)滿足I1和I2,
下面證明J(m,B,E) 滿足I3,若A1,A2∈J(m,B,E) ,且|A1|<|A2|,下面證明存在e∈A2-A1使得|(A1∪{e})∩B|≤m,從而J(m,B,E) 滿足I3。
情形一: 若|A1∩B||A2∩B|=m,存在e∈A2-B且e∈A2-A1,若不然有任意的e∈A2-B都有e∉A2-A1,即e∈A1,此時有|A1|=|A1∩B|+|A2-B|= m+|A2-B|=|A2∩B|+|A2-B|=|A2|,與|A1|<|A2|矛盾。 此時有|(A1∪{e}) ∩B|=m≤m成立。
情形二: 若|A1∩B|<m,|A2∩B|<m,對於任意的e∈A2- A1都有|( A1∪{ e} ) ∩B|≤m,即I3得證。
情形三: 若|A1∩B|>|A2∩B|,則一定存在e∈A2-A1,且有e∉B,此時有|(A1∪{e})∩B|=|A1∩B|≤m。
例1 取E = { 1,2,3,4,5} ,B = { 1,3,5} ( 本題中Jm,B= {I∈2B||I|≤m} ) ,則
J( 0,B)= {∅,{2} ,{4} ,E-B}=2E-B⊕J0,B,
J(1,B) = {∅,{1,2,4} ,{1,4} ,{1,2} ,{1} ,{2,3,4} ,{2,3} ,{3,4} ,{3} ,{2,4,5} ,{2,5} ,{4,5} ,{5} ,{2} ,{4} ,{2,4} } = 2E-B⊕J1,B,
J(2,B) = {∅,{1,2,4} ,{1,4} ,{1,2} ,{1} ,{2,3,4} ,{2,3} ,{3,4} ,{3} ,{2,4,5} ,{2,5} ,{4,5} ,{5} ,{2} ,{4} ,{2,4} ,{1,2,3,4} ,{1,2,3} ,{1,3,4} ,{1,3} ,{1,2,4,5} ,{1,2,5} ,{1,4,5} ,{1,5} ,{2,3,4,5} ,{2,3,5} ,{3,4,5} ,{3,5} }= 2E-B⊕J2,B,
類似的通過計算,可以得到
J(3,B) =2E-B⊕J3,B.
基於例1 可以發現並證明下面的廣義均勻擬陣的構造定理:
定理2 設E是一個有限集,B⊆E,m≤|B| ,則
J(m,B,E) = 2E-B⊕Jm,B.